.
Ela: Określ przedziały wklęsłości/wypukłości funkcji f(x) oraz podaj punkty przegięcia jej wykresu
f(x) = 3x5 − 10x4 + 2x
1 lis 23:57
Janek191:
f(x) = 3 x5 − 10 x4 + 2 x
więc
f '(x) = 15 x4 − 40 x3 + 2
f ''(x) = 60 x3 − 120 x2 = 60 x2*(x − 2)
zatem
dla x > 2 jest f ''(x) > 0, czyli w przedziale ( 2; +∞) funkcja f jest wypukła
dla x < 2 jest f ''(x) < 0, czyli w przedziale ( −∞; 2) funkcja f jest wklęsła
Punkt x = 2 jest punktem przegięcia wykresu danej funkcji
2 lis 06:35
Ela:
| 2 | | 1 | |
| − |
| = 0 (zał: x≠0) |
| x4 | | x2 | |
x=
√2 lub x=−
√2
funkcja jest wypukla w przedziale (−
∞,−
√2)∪ (
√2,+
∞)
funkcja jest wklęsła w przedziale {−
√2,0) ∪ (0,
√2)
Punkty x=
√2 i x=−
√2 są punktami przegięcia wykresu
2 lis 13:46
Ela: mógłby ktoś sprawdzić czy dobrze?
2 lis 13:46
Janek191:
Źle − zapomniałaś o dziedzinie

D = ( 0 ; +
∞ ) ze względu na logarytm
2 lis 13:52
Ela: zamiast x4 nie powinno byc x3?
2 lis 13:55
Janek191:
| | −2 | | 1 | | 1 | |
f '(x) = |
| + |
| = −2 x−2 + |
| |
| | x2 | | x | | x | |
| | 1 | | 4 | | 1 | |
f '' (x) = −2*(−2)*x−3 − |
| = |
| − |
| |
| | x2 | | x3 | | x2 | |
2 lis 14:04
Janek191:
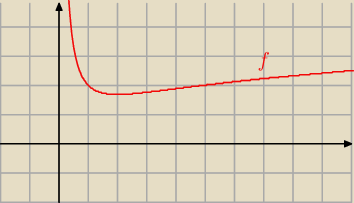
2 lis 14:11
Ela: dzięki

funkcja jest wklesla w przedziale (0,4)
wypukla (4,
∞)
punkt przegiecia x=4
f(x)=4x+x
−1
f'(x)=4−
1x2
f''(x)=
2x3
co w przypadku takiej funkcji? jak bedzie wygladala odpowiedz?
2 lis 14:15
2 lis 14:15
Janek191:
Ten wykres pewnie jednak jest zły .
2 lis 14:18
Janek191:
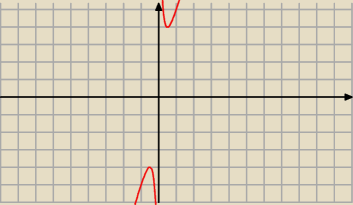
Dla x > 0 f ''(x) > 0 więc f jest wypukła.
Dla x < 0 f ''(x) < 0 więc f jest wklęsła
2 lis 14:22
Ela: dzięki

2 lis 14:29
 D = ( 0 ; +∞ ) ze względu na logarytm
D = ( 0 ; +∞ ) ze względu na logarytm

 funkcja jest wklesla w przedziale (0,4)
wypukla (4,∞)
punkt przegiecia x=4
f(x)=4x+x−1
f'(x)=4−1x2
f''(x)=2x3
co w przypadku takiej funkcji? jak bedzie wygladala odpowiedz?
funkcja jest wklesla w przedziale (0,4)
wypukla (4,∞)
punkt przegiecia x=4
f(x)=4x+x−1
f'(x)=4−1x2
f''(x)=2x3
co w przypadku takiej funkcji? jak bedzie wygladala odpowiedz?
 Dla x > 0 f ''(x) > 0 więc f jest wypukła.
Dla x < 0 f ''(x) < 0 więc f jest wklęsła
Dla x > 0 f ''(x) > 0 więc f jest wypukła.
Dla x < 0 f ''(x) < 0 więc f jest wklęsła
