. Neelly: Pochodna z f(x) = ln(x²+x−2)

	1
f'(x) =		(x2+x−2)(2x+1)
	x2+x−2

co mam źle?

Qulka: środkowy nawias wyrzuć

Neelly: dziwne, bo w ogolnie zadanie polega na zbadaniu monotonicznosci tej funkcji,

	1
wiec trzeba to pozniej przyrownac do zera wiec jedynym miejscem zerowym bedzie −
	2

w odpowiedziach natomiast miejsca zerowe tzn ekstrema to 0 i 2

Neelly: wiec odpowiedzi mam złe?

Godzio: x² + x − 2 > 0 (x + 2)(x − 1) > 0 x ∊ (−∞,−2) U (1,∞)

	1
Więc automatycznie ani 0 ani −		nie może być ekstremum bo nie należy do dziedziny.
	2

Nie ma ekstremum.

Neelly: przeprasszam, w odp esktrema to −2 i 1

Neelly: ok, dzieki

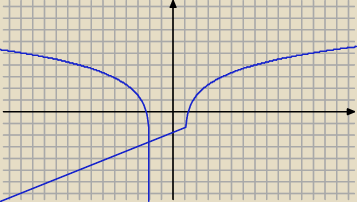
Qulka: jak widać funkcja nie ma ekstremów D: x²+x−2>0 więc x∊(−∞;−2)u(1;∞)

Qulka: ten skos to błąd programu

Neelly: Jaką w takim razie dac odpowiedz skoro polecenie brzmi: zbadaj monotonicznosc funkcji i podaj jej ekstrema? ekstremum nie ma, co z monotonicznoscia?

Godzio: Tam gdzie pochodna > 0 tam funkcja rośnie, z tym chyba już nie ma problemów ? Zadanie ze szkoły średniej

Qulka: jak widać na obrazku ..na początku maleje .. potem rośnie

Neelly:

	1
z warunku koniecznego x=−		i jest to minimum, tak?
	2

Neelly: zastanawia mnie dlaczego później w tabelce uwzgledniane sa przecięcia tylko −2 i 1, a to −¹₂ już nie

Neelly: zastanawia mnie dlaczego później w tabelce uwzgledniane sa przecięcia tylko −2 i 1, a to −¹₂ już nie

Neelly: Wszystkie przedzialy w tabelce nie powinny wygladac tak? (∞,−2), −2, (−2,−1/2), −1/2, (−1/2,1), 1, (1,∞) ?

Neelly: x2 + x − 2 > 0 to zalozenie dlatego, ze argument logarytmu naturalnego musi byc zawsze wiekszy od 0?

Neelly: x2 + x − 2 > 0 to zalozenie dlatego, ze argument logarytmu naturalnego musi byc zawsze wiekszy od 0?

Qulka: tak

Neelly: mógłby ktoś zrobić tabelkę z monotonicznością tej funkcji? nie rozumiem dlaczego w odp uwzględnione są przedziały (∞,−2) (−2,1) (1,∞) wiem, ze takie sa zalozenia, taka jest dziedzina ale nie wiem jak to sie ma do monotonicznosci?

Neelly: juz rozumiem, nie trzeba

Mila: f(x) = ln(x²+x−2) Dziedzina: x²+x−2>0⇔x<−2 lub x>1

	2x+1
f'(x)=
	x2+x−2

f'(x)=0⇔2x+1=0 i x∊D_f

	1
x=−		∉Df brak ekstremów
	2

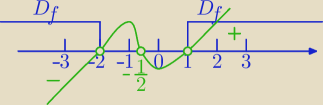
Monotoniczność (2x+1)*(x²+x−2)>0 (2x+1)*(x−1)*(x+2)>0

	1
x=−		, x=1,x=−2
	2

Rysujemy "falę", ale interesuje nas rozwiązanie nierówności tylko w dziedzinie f(x) dla x∊(−∞,−2) pochodna f'(x)<0⇔f(x) jest malejąca w tym przedziale f'(x)>0 dla x>1 ⇔f(x) jest rosnąca w tym przedziale.