Nierówności z wartością bezwzględną Awans: Rozwiąż nierówność |x−4|<|x| Nastepnie oblicz sumę jej całkowitych rozwiązań mniejszych od 15.

5-latek:

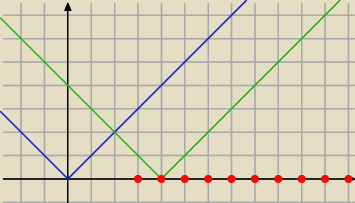
Qulka: zielona < niebieskiej 3+4+5+6+7+8+9+10+11+12+13+14 = 62

PW: Można też rozwiązać korzystając z geometrycznej interpretacji na osi. |x − a| oznacza, jak wiadomo, odległość od liczby x do liczby a. Wobec tego zadana nierowność |x − 4| < |x − 0| oznacza "liczbie x jest bliżej do 4 niż do zera", co daje jako zbiór rozwiązań przedział (2,∞). Rozwiazania określone w zadaniu są oczywiście takie jak podała Qulka.

Eta: 3+4+5+........+14= 17*6=102

PW: Rozwiązania takie, suma − nie. Nawet mi do głowy nie przyszło sprawdzać sumowanie po tak szacownym przedmówcy

Qulka: oj tam ..przecież 9+11 może się równać 10 jak się tylko patrzy na 10 i liczy w jeden bok

pigor: ..., M−u, oczywiście że możesz np. tak: : |x−4|<|x| i (*) x<15 ⇒ (x−4)²< x² ⇔ x²−8x+16−x²< 0 ⇔ 8x >6 ⇒ x >2 , stąd i z (*) 2< x< 15 , więc suma liczb liczona jak mały G. (3+14) +4+13 +5+12 +6+11 +7+10 +8+9= 6*17= 60+42= 102...

PW: pigor pisze jakieś tajemnicze listy do M*, zauważyliście?

pigor: ..., no właśnie do przesympatycznej panny M−i ,której nie mogę, nie potrafię, a tak naprawdę... nie chcę odmówić .