równanie trygonometryczne Marusia: oblicz sumę wszystkich rozwiązań równania 1.sinx=0,7 które należą do przedziału <0;6π>

	π
przyjęłam, że dla x1=
	4

	3π
x2=
	4

następnie dla x₁sumowałam

π		π		π
	+(		+2π)+(		+4π)
4		4		4

tak samo dla x₂ i razem wyszło 15π jak to zapisać prościej?

	1
2. cosx=		które należą do przedziału<−4π;4π>
	3

	7π
z tablic odczytałam≈700 więc,przyjąć		?
	18

Pomóżcie, proszę.....

Marusia: nikt nie pomoże?

PW:

	π
Jaki związek z sinx = 0,7 mają rozważania o liczbie x1 =		?
	4

Marusia:

	π
odczytałam z tablic, że sin 45o ≈0,7 a 45o to
	4

PW: Wiem, że pokazujesz coś "na pobliskim naprzykładzie", ale powinno być opisane tak: Dla dowolnej liczby u∊(0, 1), w szczególności dla u = 0,7, istnieją w przedziale (0, 2π> dwa rozwiązania równania sinx = u spełniające zależność

	π		π
		− x1 = x2 −		,
	2		2

inaczej x₁ + x₂ = π. Tu przyda się rysunek − ilustracja tego faktu na wykresie. Teraz można sumować wszystkie rozwiązania na przedziale <0, 6π> − jest ich 3 razy więcej niż na przedziale (0, 2π>.

Marusia: no to ja tego nie rozumiem, chociaż wynik wyszedł mi dobry. Można to jakoś prościej wytłumaczyć?

PW: Uściślę ostatnie zdanie, bo "trzy razy więcej" niewiele znaczy. Suma rozwiązań leżących w przedziale (2π, 4π> jest równa x₁+ 2π x₂ + 2π = x₁ + x₂ + 4π = π + 4π = 5π, a suma rozwiazań leżących w przedziale (4π, 6π> jest równa x₁+4π + x₂ + 4π = 9π. Twoja odpowiedź była dobra, ale nie poprawna (uzyskana na przykładzie), na szczęście dla wszystkich rozwiązań suma w przedziale (0,2π> jest równa π.

Marusia: W drugim zadaniu drogą dedukcji (nie wiem czy słuszną) wychodzi mi 0 bo x leżą po obu stronach osi OY

Marusia: Teraz do mnie dotarło... A w drugim zadaniu?

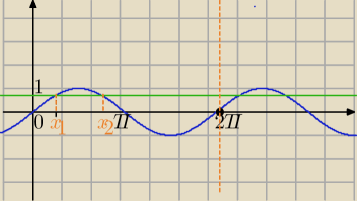
Mila: sinx=0.7 równanie to ma dwa rozwiązania w przedziale <0,2π>

	π
Niech x0 będzie rozwiązaniem z przedziału (0,		)
	2

to masz serię rozwiązań : x₁=x₀+2kπ , x₂=π−x₀+2kπ W takim razie : dla k=0 przedział <0,2π> x₁=x₀ , x₂=π−x₀ x₁+x₂=x₀+π−x₀=π k=1 przedział (2π,4π) x₃=x₀+2π x₄=π−x₀+2π=3π−x₀ k=2 przedział (4π,6π) x₅=x₀+4π x₆=π−x₀+4π=5π−x₀ Teraz oblicz sumę : 15π

PW: Myślisz poprawnie, ale opis trzeba udoskonalić (słowo pisane musi się samo obronić). Funkcja cosx jest parzysta. Oznacza to, że dla każdego rozwiązania równania

	1
cosx =
	3

należącego do przedziału (0, 4π> istnieje drugie rozwiązanie (będące liczba przeciwną) należące do przedziału <−4π, 0). Suma liczb przeciwnych jest równa zeru, wobec tego suma wszystkich rozwiązań (niezależnie od tego ile ich jest) jest zerem.

Marusia: Nie umiałam myśli ująć w słowa. Super wytłumaczone. Jeszcze mam jeden (oby tylko jeden) problem:

	9		15
w zadaniu Podaj miejsca zerowe funkcji f(x)=cos x należące do przedziału (−		;		)
	2		2

jak ten przedział przeliczyć na π?

PW: Na szczęście miejsca zerowe funkcji cosx zdarzają się "rzadko" (wiemy co ile), a wiec wystarczy badany przedział zastąpić przedziałem o końcach wyrażonych za pomocą π, niewiele różniących się od podanych. Wiemy, że 3,14 < π < 3,15. Wynika stąd, że

	5		5
		π <		·3,15
	2		2

	5		15,75
		π <		.
	2		2

O drugim krańcu pomyśl podobnie.

Mila:

	π
cosx=0⇔x=		+kπ
	2

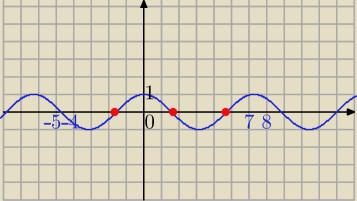
Najlepiej z wykresu: Raczej podstaw za π i oblicz k∊C 2) Możesz też rozwiązać nierówność:

	9		π		15		π
−		<		+kπ<		/−
	2		2		2		2

	9		π		15		π
−		−		<kπ<		−		/:π
	2		2		2		2

	9		1		15		1
−		−		<k<		−
	2π		2		2π		2

Marusia: zrobiłam do wspólnego mianownika

−9−π		15−π
	<k<
2π		2π

i niestety dalej nie umiem.