dziedzina logarytmicznej funkcji olla: Wiem, że a musi być liczbą rzeczywistą dodatnią i różną od 1 oraz x jest liczbą rzeczywistą dodatnią. W tym przykładzie mam jednak problem podejrzewam,że źle rozwiązuję przykład i dlatego mi nie wychodzi; f(x)=log₃(log₂(x+1)) wyszła mi dziedzina x>−1 bo 3>0 i różne od 1 tak samo 2 więc x+1>0 czyli x>−1 i jest źle proszę o pomoc

Aga1.: x+1>0 i log₂(x+1)>0

olla: no to wychodzi mi x> −1 w odpowiedzi jest inaczej a w drugim 2⁰>x+1 i x>0 i cześć wspólna jest dziedziną czyli x>0 tak?

olla: a tu jak? √log(2+x)−log(5−x) liczba pod pierwiastkiem większa musi być od 0, ale podzielić to czy 2+x>0 i 5−x>0 nonsens

5-latek: 2+x>0 i 5−x>0 log(2+x)−log(5−x)≥0 log(2+x)−log(5−x) ≥log1 bo log1=0 bo 10⁰=1

2+x
	≥1 ale to zosatwiam już Tobie i potem wyznaczasz czesc wspolna tych 3
5−x

rozwiazan

olla: no tak podstawa 10 co za plama, dzięki dalej wiem

olla: a ten pierwszy przykład jest dobrze ?

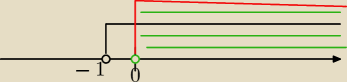
5-latek: Widzisz najlepiej to sobie te warunki narysować na osi liczbowej

Aga1.: log₂(x+1)>0 log₂(x+1)>log₂2⁰ x+1>1, a nie jak napisałaś 0 22:33 2⁰>x+1 x>0

Aga1.: A nierówność log(2+x)−log(5−x)≥0 można rozwiązać tak log(2+x)≥log(5−x) 2+x≥5−x dokończ