Korzystanie ze wzooru de Moivrea in.: Korzystanie ze wzooru de Moivrea (⁵√2−⁵√2)⁶ wiem co mam po kolei robic ale nie umiem obliczyc modułu z tego.

Qulka: 2^7/10

in.: a czemu tak?

Qulka: bo moduł to √a²+b²

Mila: To chyba bez sensu podnosić zero do 6 potęgi za pomocą wzorów.

Qulka: ja podejrzewam, że zapomniał dopisać i więc na wszelki wypadek je sobie tam wstawiłam

in.: w sensie 2¹/5 − 2¹/5 i to wszystko pod pierwsiatekiem. i jak to wychdozi 2 7/10?

in.: chodzmi mi o kwestie odejmowanie liczb o tych samych potęgach i wykladnikach

Qulka: a²+b²=2^2/5+2^2/5 = 2•2^2/5=2^7/5 pierwiastek z tego daje 2^7/10

Qulka: nie ma wzorów na dodawanie i odejmowanie potęg

in.: aaa dobra juz wiem gdzie popełniłam bład. tam nie powinnpo byc minusa. dzięki wilekie

Mila: (⁵√2−⁵√2*i)⁶=[⁵√2*(1−i)]⁶= =⁵√2⁶*(1−i)⁶=⁵√2⁶*(1−i)⁶ zajmiemy się z=1−i z=1−i |z|=√1²+1²=√2

	π		7π
φ=2π−		=
	4		4

	7π		7π
25√2*(1−i)6 =25√2*√26*[cos(6*		)+i *sin(6*		)]=
	4		4

	21π		21π
=165√2*(cos		+i*sin		)=
	2		2

	π		π
=165√2*(cos(10π+		)+i sin(10π+		)=165√2*(0+i)=165√2i
	2		2

To samo otrzymasz szybciutko bez wzoru: ⁵√2⁶*((1−i)²)³=2⁵√2*(1−2i+1)³=2⁵√2*(−2i)³= =2⁵√2*(−2)³*i³=2⁵√2*(−8)*(−i)=16⁵√2 i

in.: chcoiaz pózniej cos i tak nie wychodzi bo mi wyszedl − pierwiastek z 2. a powinien byc traki zeby go odczytac z tabelki fubkcji trydgo na 30 45 60 90

in.: mila a skad to 1−i na samym poczatku?

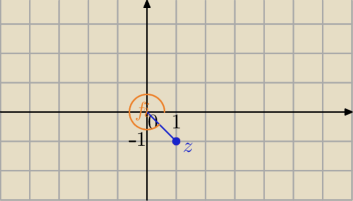
Mila: Przecież napisałam− wyłączyłam ⁵√2 przed nawias, zobacz pierwszą i drugą linijkę. Kąt masz narysowany, taki sam będzie dla P= (⁵√2,−⁵√2) jak i dla P'=(1,−1) Liczba z=(⁵√2−⁵√2*i) to punkt P= (⁵√2,−⁵√2) na płaszczyźnie z ukł. wsp. Jeśli liczysz kąt , to tak: |1−i|=√2

	1		√2
cosφ=		=
	√2		2

	−1		√2
sinφ=		=−
	√2		2

	7π
φ=
	4