>>> oliwka77: Obwód trapezu równoramiennego jest równy 30 cm, a odcinek łączący środki przekątnych trapezu ma długość 1, 5 cm. Wiedząc że w ten trapez można wpisać okrąg oblicz: a) długość podstawy trapezu b) długość średnicy okręgu wpisanego w ten trapez c) długość odcinka łączącego punkty stycznośći ramion z tym okręgiem

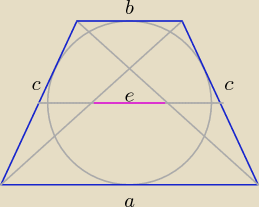
Bogdan: a) Ponieważ w trapez można wpisać w okrąg, to a + b = 2c a + b + a + b = 30 ⇒ a + b = 15

	a − b
e =		⇒ a − b = 2e ⇒ a − b = 3
	2

Rozwiąż układ równań: a + b = 15 i a − b = 3

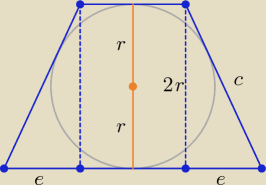Bogdan: Po wyznaczeniu w punkcie a) długości podstaw a oraz b z równości a + b = 2c wyznacz c,

	a − b
z równości e =		wyznacz e, wreszcie korzystając z twierdzenia Pitagorasa wyznacz
	2

2r.

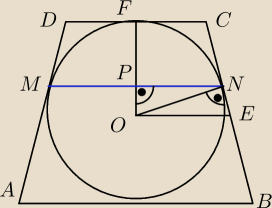B: c) |OF| = |ON| = r = 1.5√6 − policzone w poprzednim podpunkcie |OE| = ¹₂ * ^a+b₂ = 3.75 ΔONE ~ ΔOPN (kkk) |∡ONE| = |∡OPN| |∡NOE| = |∡PNO| zatem, ^||PN|_|ON| = ^|ON|_|OE| ⇒ ^|PN|_{1.5 √6} = ^{1.5 √6}_3.75 ⇒ 3.75 * |PN| = 13.5 ⇒ |PN|=3.6 |MN| = 2 * |PN| = 2 * 3.6 = 7.2

magda: skąd wiemy, że e=(a−b)/2 ?

Eta:

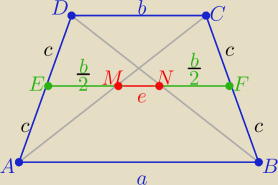
	a+b
|EF|=		−− długość linii środkowej trapezu
	2

Z podobieństwa trójkątów ADC i AEM oraz BCD i BFN w skali k=2

	b
wynika,że |EM|=|NF|=
	2

	b		a+b		2b		a+b−2b		a−b
to e=|EF|−2*		⇒ e=		−		=		=
	2		2		2		2		2

	a−b
e=
	2