x
x: Czesc, mam problem z zadaniem z parametrami.
Tresc brzmi tak:
Dla jakich wartosci parametru "m" rownanie ma dwa rozne pierwiastki, ktore są liczbami
dodatnimi?
x2−(m+2)x+m+5=0
A zaczelam tak:
∆>0
a=1, b=−(m+2), c=m+5
∆=b2−4*a*c
∆=(−(m+2))2−4*1*(m+5)=m2+4m+4−4m−20=m2−16>0
(m+4)(m−4)>0
m>4 ∩ m<−4
m∈ (−∞;−4) U (4;+∞)
I dalej nie wiem co mam począć o ile do tej pory jest wszystko ok?
31 paź 20:47
sushi_gg6397228:
wzory Viete'a się kłaniają
31 paź 20:49
x: Specjalnie uczylam sie tego materialu dzisiaj o tych wzorach, bo moja sytuacja wyglada tak, ze
jestem w 2 kl liceum zaocznej (przez zawodowke 3 letnia, automatycznie przeskoczylam do 2 kl
liceum), ale jednak musze napisac prace na zaliczenie tej 1 kl liceum, tak wiec i material
widze pierwszy raz na oczy.
Wracajac do tematu... Mam to zrobic tak?
x1*x2>0 ∩ x1*x2 >0
c/a>0 ∩ −b/a>0
m+5/1>0 ∩ m+2/1>0
m/1>−5 ∩ m/1>−2
m>−5 ∩ m>−2
No i tutaj juz mam pustke w glowie, bo nie wiem co i jak.
31 paź 20:56
sushi_gg6397228:
spójnik wyglada tak ⋀, tamten jest do zbiorów
odnośnie Δ
(m+4)(m−4) >0 to po prostu rysujesz parabole, a nie tak po chińsku przekształcasz
popraw zapisy i jeszcze raz
31 paź 20:58
x: Apropo jeszcze paraboli, ma byc rosnąca?
31 paź 21:01
sushi_gg6397228:
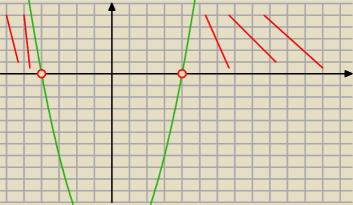
y= m
2− 16 parabola uśmiechnięta
każda parabola jest do polowy rosnąca, do połowy malejąca

31 paź 21:07
x: No niby tak, ale uczono mnie, ze tak wygląda rosnąca wlasnie

.
x1*x2=m+5
x1+x2=m+2
Co nalezy zrobic nastepnie?
31 paź 21:10
sushi_gg6397228:
Aby było porządnie, to trzeba wypisać warunki
1. Δ >0
⋀
2. x
1*x
2 >0
⋀
3. x
1+x
2 >0
1. masz policzone
2 i 3 to jakoś po chińsku liczysz
m+5/1>0 ∩ m+2/1>0
m/1>−5 ∩ m/1>−2 <−− kto tak uczył robić
spójniki ⋀
od nowa
31 paź 21:14
x: Nikt nie uczyl tak robic, bo dzis sie sama na wlasna reke uczylam, bo nigdy na zajeciach tego
nie mialam, wiec musisz wybaczyc mi bledy

.
Dobra, od początku napisze calosc, ale pewnie znow cos zle zrobie.
x2−(m+2)x+m+5=0
1. Δ >0
⋀
2. x1*x2 >0
⋀
3. x1+x2 >0
∆>0
a=1, b=−(m+2), c=m+5
∆=b2−4*a*c
∆=(−(m+2))2−4*1*(m+5)=m2+4m+4−4m−20=m2−16>0
(m+4)(m−4)>0
[tu rysunek paraboli]
m∈ (−
∞;−4) U (4;+
∞)
Tak?
31 paź 21:30
sushi_gg6397228:
2. 3. było nierówności, nierozwiazane
do dzieła
obliczenia OK
31 paź 21:35
x: Poczekaj, bo juz sie pogubilam to co ja mam teraz zrobic? Mam tylko te znaki zmienic? Zamiast
"=" wpisac ">"?
31 paź 21:38
sushi_gg6397228:
x1*x2 >0
m+5>0
...
x1+x2 >0
m+2>0
...
31 paź 21:44
x: Aaaa, dobra, juz wiem

.
x2−(m+2)x+m+5=0
1. Δ >0
⋀
2. x1*x2 >0
⋀
3. x1+x2 >0
∆>0
a=1, b=−(m+2), c=m+5
∆=b2−4*a*c
∆=(−(m+2))2−4*1*(m+5)=m2+4m+4−4m−20=m2−16>0
(m+4)(m−4)>0
[tu rysunek paraboli]
m∈ (−
∞;−4) U (4;+
∞)
x1*x2>0
m+5>0
m>−5
x1+x2>0
m+2>0
m>−2
?
31 paź 21:50
sushi_gg6397228:
masz trzy rozwiązania dla "m"
na jedna oś i część wspolna
31 paź 21:51
x: Wytlumacz jakos jasniej jak do blondynki...
31 paź 21:53
sushi_gg6397228:
z kazdego warunki dostalas jakaś nierownosc m>− 5 m>−2 m .....
teraz trzeba to zebrac i dac ostateczna odpowiedz
31 paź 21:59
x: To ma jakiś zwiazek z ta wczesniejsza czworka?
31 paź 22:00
x: Jezu, nie wiem, nie ogarniam tego do konca, do tej pory jakos szlo, ale teraz to juz nie mam
zielonego pojecia...
31 paź 22:01
sushi_gg6397228:
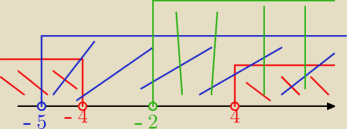
robisz np tak
i teraz patrzysz gdzie trzy kolory sie pokrywaja
31 paź 22:06
Jolanta:

narysuj os liczbowa i na niej zaznacz np jeżeli m>7 i m<11 to rozwiazaniem jest (7,11) cześć
wspólma
31 paź 22:09
x: No dobrze − tu jest m∊(4,+∞). Czyli by to wyznaczyc to mam zrobic taki wykres z tymi
wczesniejszymi wyznaczonymi i dolozyc te rozwiązania z sumy i iloczynu?
31 paź 22:10
sushi_gg6397228:
a co zrobilem o 22.06 ?
31 paź 22:18
x: No wlasnie to, tylko pytam na bieżąco by się nie pogubic i by to zrozumiec... Ok, to bedzie
potem ten rysunek, pod nim m∊(4,+∞), a co trzeba zrobic dalej?
31 paź 22:24
Jolanta: Jeżeli masz warunek ze ma być i to i to rozwiazaniem jest wspólna część z rysunku odczytaj
jakie ma być m .(Muszą sie wszystkie kolory pokryć}
31 paź 22:30
x: No ja juz calkiem zglpialam... m=4?
31 paź 22:32
sushi_gg6397228:
m>4 czesc wspolna lub jak kto woli m ∊(4; ∞)
31 paź 22:35
x: Czyli cale zadanie od gory do dolu ma wygladac tak:
x2−(m+2)x+m+5=0
1. Δ >0
⋀
2. x1*x2 >0
⋀
3. x1+x2 >0
∆>0
a=1, b=−(m+2), c=m+5
∆=b2−4*a*c
∆=(−(m+2))2−4*1*(m+5)=m2+4m+4−4m−20=m2−16>0
(m+4)(m−4)>0
[tu rysunek paraboli]
m∈ (−∞;−4) U (4;+∞)
x1*x2>0
m+5>0
m>−5
x1+x2>0
m+2>0
m>−2
[tu kolejny rysunek z wyznaczeniem czesci wspolnej]
m>4
?
I to zadanie jest juz zakonczone, tak?
31 paź 22:38
sushi_gg6397228:
odpowiedz do zadania: m>4
31 paź 22:42
Jolanta:

po prawej stronie od 4 wzwyz masz spełnione wszystkie warunki m>−5 i m>−2 im>4
31 paź 22:43
x: Jutro jeszcze to sobie przeanalizuje, by zrozumiec o co chodzi, a tymczasem bardzo dziękuję za
pomoc i cierpliwosc, dobranoc

.
31 paź 22:44
sushi_gg6397228:
1.
∆>0
a=1, b=−(m+2), c=m+5
∆=b2−4*a*c
∆=(−(m+2))2−4*1*(m+5)=m2+4m+4−4m−20=m2−16>0
(m+4)(m−4)>0
[tu rysunek paraboli]
m∈ (−∞;−4) U (4;+∞)
2.
x1*x2>0
m+5>0
m>−5
3.
x1+x2>0
m+2>0
m>−2
[tu kolejny rysunek z wyznaczeniem czesci wspolnej]
m>4
31 paź 22:45
sushi_gg6397228:
na zdrowie

kolorowych...
31 paź 22:45
Mila:
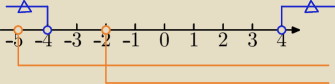
x
2−(m+2)x+m+5=0
1)Δ>0 (istnieją dwa różne pierwiastki ( rozwiązania))
2) x
1*x
2>0 i x
1+x
2>0 ⇔x
1>0 i x
2>0
−−−−−−−−−−−−−−−−−−−−−−
Ad 1)
Δ=(m+2)
2−4*(m+5)=m
2+4m+4−4m−20
Δ=m
2−16
m
2−16>0⇔
(m−4)*(m+4)>0 zaznaczone na osi Δ>0⇔
m<−4 lub m>4
Ad 2)
m+2>0 i m+5>0⇔
m>−2 i m>−5⇔
m>−2
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
(1) i (2) część wspólna
m>4
Odp.
m>4⇔m∊(4,
∞)
==============
31 paź 22:49
 y= m2− 16 parabola uśmiechnięta
każda parabola jest do polowy rosnąca, do połowy malejąca
y= m2− 16 parabola uśmiechnięta
każda parabola jest do polowy rosnąca, do połowy malejąca 
 .
x1*x2=m+5
x1+x2=m+2
Co nalezy zrobic nastepnie?
.
x1*x2=m+5
x1+x2=m+2
Co nalezy zrobic nastepnie?
 .
Dobra, od początku napisze calosc, ale pewnie znow cos zle zrobie.
x2−(m+2)x+m+5=0
1. Δ >0
⋀
2. x1*x2 >0
⋀
3. x1+x2 >0
∆>0
a=1, b=−(m+2), c=m+5
∆=b2−4*a*c
∆=(−(m+2))2−4*1*(m+5)=m2+4m+4−4m−20=m2−16>0
(m+4)(m−4)>0
[tu rysunek paraboli]
m∈ (−∞;−4) U (4;+∞)
.
Dobra, od początku napisze calosc, ale pewnie znow cos zle zrobie.
x2−(m+2)x+m+5=0
1. Δ >0
⋀
2. x1*x2 >0
⋀
3. x1+x2 >0
∆>0
a=1, b=−(m+2), c=m+5
∆=b2−4*a*c
∆=(−(m+2))2−4*1*(m+5)=m2+4m+4−4m−20=m2−16>0
(m+4)(m−4)>0
[tu rysunek paraboli]
m∈ (−∞;−4) U (4;+∞)
 .
x2−(m+2)x+m+5=0
1. Δ >0
⋀
2. x1*x2 >0
⋀
3. x1+x2 >0
∆>0
a=1, b=−(m+2), c=m+5
∆=b2−4*a*c
∆=(−(m+2))2−4*1*(m+5)=m2+4m+4−4m−20=m2−16>0
(m+4)(m−4)>0
[tu rysunek paraboli]
m∈ (−∞;−4) U (4;+∞)
x1*x2>0
m+5>0
m>−5
x1+x2>0
m+2>0
m>−2
?
.
x2−(m+2)x+m+5=0
1. Δ >0
⋀
2. x1*x2 >0
⋀
3. x1+x2 >0
∆>0
a=1, b=−(m+2), c=m+5
∆=b2−4*a*c
∆=(−(m+2))2−4*1*(m+5)=m2+4m+4−4m−20=m2−16>0
(m+4)(m−4)>0
[tu rysunek paraboli]
m∈ (−∞;−4) U (4;+∞)
x1*x2>0
m+5>0
m>−5
x1+x2>0
m+2>0
m>−2
?
 robisz np tak
i teraz patrzysz gdzie trzy kolory sie pokrywaja
robisz np tak
i teraz patrzysz gdzie trzy kolory sie pokrywaja
 narysuj os liczbowa i na niej zaznacz np jeżeli m>7 i m<11 to rozwiazaniem jest (7,11) cześć
wspólma
narysuj os liczbowa i na niej zaznacz np jeżeli m>7 i m<11 to rozwiazaniem jest (7,11) cześć
wspólma
 po prawej stronie od 4 wzwyz masz spełnione wszystkie warunki m>−5 i m>−2 im>4
po prawej stronie od 4 wzwyz masz spełnione wszystkie warunki m>−5 i m>−2 im>4
 .
.
 kolorowych...
kolorowych...
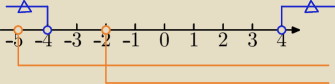 x2−(m+2)x+m+5=0
1)Δ>0 (istnieją dwa różne pierwiastki ( rozwiązania))
2) x1*x2>0 i x1+x2>0 ⇔x1>0 i x2>0
−−−−−−−−−−−−−−−−−−−−−−
Ad 1)
Δ=(m+2)2−4*(m+5)=m2+4m+4−4m−20
Δ=m2−16
m2−16>0⇔
(m−4)*(m+4)>0 zaznaczone na osi Δ>0⇔m<−4 lub m>4
Ad 2)
x2−(m+2)x+m+5=0
1)Δ>0 (istnieją dwa różne pierwiastki ( rozwiązania))
2) x1*x2>0 i x1+x2>0 ⇔x1>0 i x2>0
−−−−−−−−−−−−−−−−−−−−−−
Ad 1)
Δ=(m+2)2−4*(m+5)=m2+4m+4−4m−20
Δ=m2−16
m2−16>0⇔
(m−4)*(m+4)>0 zaznaczone na osi Δ>0⇔m<−4 lub m>4
Ad 2)