Najwieksza wartosc pola prostokata .: Wyznacz najwieksza wartosc pola prostokata, ktorego dwa wierzcholki leza na paraboli y=x²−4x+4, a dwa pozostale na cieciwie paraboli wyznaczonej przez prosta y=3.

.: Ktos pomoze ?

Janek191:

	4
p =		= 2
	2

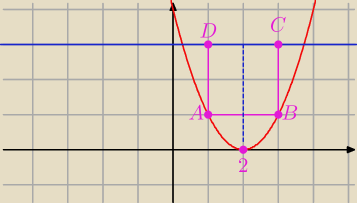
B = ( x; y) C = ( x; 3) więc P = I AB I* I BC I = 2*( x − 2)*(3 − y) ; y = x² − 4 x + 4 więc P(x) = (2 x − 4)*( 3 − x² + 4 x − 4) = (2 x − 4)*( − x² + 4 x −1 ) = = − 2 x³ + 8 x² − 2 x + 4 x² − 16 x + 4 = − 2 x³ + 12 x² − 18 x + 4 P '(x) = − 6 x² + 24 x − 18 = 0 ⇔ −6*( x² − 4 x + 3) = 0 ⇔ x = 3 P''(x) = −12 x + 24 P''(3) = −12*3 + 24 < 0 więc funkcja P(x) osiąga w x = 3 maksimum lokalne. P_max = P(3) = − 2*3³ + 12*3² − 18*3 + 4 = − 54 + 108 − 54 + 4 = 4

.: Janek191: skad masz (2x−4)*(3−x²+4x−4) ?

.: aaaaa podstawiles za y, x²−4x+4. Ok rozumiem

Janek191: Wszystko już jasne ? Tam jest też II pochodna.

Janek191: Wszystko już jasne ? Tam jest też II pochodna.

.: Wlasnie, wytlumacz mi prosze dlaczego dwa razy liczysz pochodna

Janek191: P '' − to II pochodna ( lub pochodna II rzędu ). Służy do wyznaczania m.in.: maksimum lub minimum funkcji w punkcie.

.: Ok, to my szukamy maksimum w x=3 ?

Janek191: P'( 3) = 0 , więc dla x = 3 funkcja P ma maksimum lub minimum lokalne. Ponieważ druga pochodna w tym punkcie jest ujemna : P ''(3) < 0 więc funkcja P osiąga w x = 3 maksimum. Rysunek mi się udał, bo B = ( x; y) = ( 3 ; 1)

.: Janek191, dziekuje bardzo

.: Ale powiedz jeszcze dlaczego |AB|*|BC|= 2(x−2)(3−y) ?

.: A nie dobra, juz wiem

.: Nie czekaj, dlaczego |AB|*|BC|=2(x−2)(3−y)?

Janek191: Pierwszą współrzędną punktu B jest x więc połowa długości I AB I = ( x − p) = ( x − 2) I A B I = 2*( x − 2) Szerokość prostokąta I BC I = 3 − y, bo drugą współrzędną C jest 3, a drugą współrzędną A jest y. ( y > 0)

.: Aaaaa dziekuje bardzo