geometria płaska
xxx: w jaki sposób rozwiazuje się takie zadanie
Przeciwprostokątna jednego trójkąta prostokątnego jest jednocześnie przyprostokątną drugiego
trójkąta prostokątnego. Na bokach tych trójkątów zbudowano cztery kwadraty, których pola są
odpowiednio równe P
1, P
2, P
3, P
4 (zobacz rysunek obok). Prawdziwa jest zależność:
A. P
1 + P
2 = P
3 + P
4
B. P
1 − P
2 = P
3 + P
4
C. P
2 + P
3 = P
1 + P
4
D. P
4 − P
3 = P
1 − P
2
jak to zrobić? rachunkowo czy na oko?
pomoże ktoś?
31 paź 09:40
dero2005:
Gdzie ten rysunek?
31 paź 10:08
xxx:
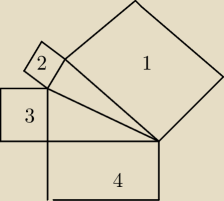
Przepraszam, zapomniałam dodać rysunek
W środku trójkąty są prostokątne a po bokach są
kwadraty
31 paź 10:32
Aga1.: odp b.
31 paź 10:38
xxx: ale dlaczego? jak to policzyłaś?
31 paź 10:41
Aga1.:
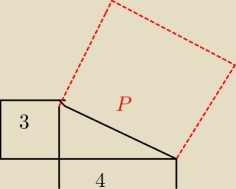
P=P
3+P
4 i P+P
2=P
1
P=P
3+P
4
P=P
1−P
2
stąd P
1−P
2=P
3+P
4
31 paź 10:44
Godzio:
Jeżeli boki trójkątów oznaczymy: a,b,c oraz d,e,c to mamy zależność:
a2 + b2 = c2 oraz e2 + f2 = c2
Przyrównując
a2 + b2 = e2 + f2 −− a to są odpowiednie Pola
P4 + P3 = P1 + P2
Odp: A
31 paź 10:46
Godzio: Źle doczytałem ... Bzdurę napisałem
31 paź 10:46
xxx: nie rozumiem
a gdzie się zgubił jeszcze jeden kwadrat? przecież to nie może wejść w skład P
31 paź 11:03
31 paź 11:28
Aga1.:
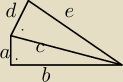
To tak jak podpowiedział Godzio
Niech P
3=a
2, P
4=b
2 P
2=d
2 i P
1=e
2, P=c
2
Z twierdzenia Pitagorasa
a
2+b
2=c
2
i
c
2+d
2=e
2⇒c
2=e
2−d
2
i dalej
c
2=e
2−d
2
c
2=a
2+b
2, stąd
e
2−d
2=a
2+b
2,czyli
P
1−P
2=P
3+P
4
31 paź 15:32
xxx: dziękuję Ci bardzo bardzo mocno
teraz rozumiem
1 lis 07:58
