Prosze o pomoc .: Dla jakich wartosci parametru a parabola o rownaniu y=ax²−5ax−2 wycina ze stycznej do krzywej o rownaniu y=(2x−3)/(x−1) w punkcie P o odcietej x=2 odcinek, ktorego srodkiem jest punkt P? W ogole nie rozumiem tego zadania

J: Na poczatek trzeba wyznaczyć równanie tej stycznej

.: Co to znaczy "wycina ze stycznej do krzywej"?

J: tzn....parabola tak przecina styczną,ze wycina z niej odcinek,którego srodkiem jest punkt P

.: Moglbys/moglabys narysowac zebym bardziej zrozumial?

J: najpierw zajmijmy się styczną ..musimy mieć jej równanie

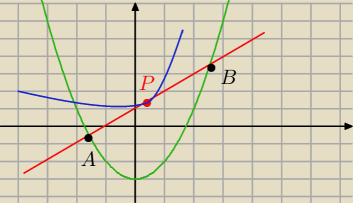
J: Niebieska, to podana funkcja, zielona parabola , P jest środkiem odcinka AB

.: Styczna do krzywej y=f(x) w punkcie A=(x₀,f(x₀)) okreslona jest rownaniem: y−y₀=f'(x₀)(x−x₀). Wiem jak liczyc pochodna, ale co mam podstawic?

J: masz podane: x₀ = 2

.: Dzieki za rysunek. Juz troche bardziej rozumiem.

.: y−y₀=f'(2)(x−2) ?

.: f'(2x−2)=2 y−y₀=2

.: A co jest y₀?

J:

	2x−3
źle liczysz styczną .. popatrz na funkcję : y =
	x−1

.: Jaki jest punkt stycznosci z ta funkcja?

.: P=(2,y)

J: x₀ = 2

J: jakie masz równanie stycznej ?

.: Taak czyli ze punkt P=(x,y), gdzie x=2 ale co z y−kiem?

===:

	2x−3
f(x)=
	x−1

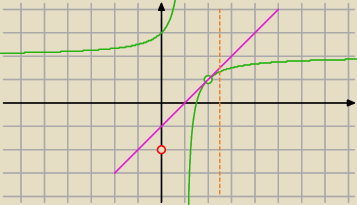
f(2)=1

	2(x−1)−(2x−3)		1
f'(x)=		=
	(x−1)2		(x−1)2

f'(2)=1 Oś symetrii Twojej paraboli to x=2,5 Przechodzi ona przez A=(0,−2) dalej proste rachunki

.: Bo styczna :y−y₀=f'(x₀)(x−x₀). Mamy juz x₀.

.: To jakie jest to rownanie stycznej do krzywej?

J: y = x − 1

===: równanie stycznej to y−1=1(x−2) ⇒ y=x−1

.: Ok super, czyli ze P=(2,1)

J: tak , to punkt P

.: Ok to mamy styczna i punkt P.

.: To teraz trzeba obliczyc a z paraboli

.: To teraz jak mam obliczyc te a jezeli tylko mam punkt P i wiem ze ta parabola przechodzi przez punkt (0,−2)?

J: skorzystaj z faktu, że wierzchołek ma odciętą : x_w = 2,5

.: Jak to obliczyles/obliczylas?

.: y=ax²−5ax−2 Mamy (0,−2) i (2.5,y). Dalej nie moge wyznaczyc a

===:

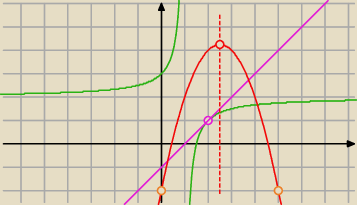
Tadeusz: ... widzę,że nie masz ochoty dokończyć A że zadanko ciekawe ... to chyba warto Przyrównując szukaną parabolę i styczną (ich równania) ax²−5ax−2=x−1 otrzymamy iksowe współrzędne punktów przecięcia. Nie interesują nas ich wartości ... wykorzystamy zaś fakt, że: x=2 jest osią symetrii dla g(x)=ax²−5ax−x−2+1 g(x)=ax²−(5a+1)x+1

	5a+1
zatem 2=		⇒ a=−1
	2a

.: Patrz, nooo teraz sie zgadza. Dziekuje bardzo Tadeusz

Tadeusz: duży rośnij