nierownosc logarytmiczna
dawsonika: rozwiaz nierownosc:
logx4< 8
29 paź 11:05
Tadeusz:
| 1 | |
| <8 itd  |
| log4x | |
29 paź 11:16
J:
zrób jeszcze założenia: x > 0 i x ≠ 1
29 paź 11:18
dawsonika: i i jak dalej ? nie bardzo rozumiem w czym mi ma pomoc odwrotnosc logx4 , ktora zostala
wprowadzona mimowolnie bez zadnej podstawy prawnej
29 paź 11:20
Tadeusz:
... to chyba nie znasz "prawa"
29 paź 11:22
Tadeusz:
chyba też nie znasz znaczenia słowa mimowolnie
29 paź 11:24
J:
dla Ciebie podstawą jest: "prawo ucznia"
29 paź 11:25
Tadeusz:
nie chcesz zmieniać .... możesz rozwiązywać dla: 0<x<1 i x>1
29 paź 11:29
dawsonika: Nic z tego nie rozumiem. Jak 0<x<1 ma sie do mojej nierownosci ? Pokaz 1 caly konretny krok bo
nie moge wlasnie tego zrozumiec
29 paź 11:31
Tadeusz:
... to przeczytaj rozdział o logarytmach ... a założeniach ... o przebiegu funkcji
logarytmicznej
29 paź 11:33
29 paź 11:34
J:
... ⇔ logx4 < logxx8
dla: x ∊ (0,1) ...... ⇔ 4 > x8
dla: x > 1 ...... ⇔ 4 < x8
29 paź 11:35
dawsonika: Przejzalem wszystkie te podpunkty i nigdzie nie ma przedstawionego przykladu ,ze to x jest
podstawa logarytmu
29 paź 11:36
dawsonika: no tak myslalem , ale jak rozwiazac takie rownanie ,ze x jest az w 8 potedze
29 paź 11:36
Tadeusz:
żarty stroisz?
Ty już jesteś ciut nie maturzysta
29 paź 11:41
J:
zamień liczbę 4 na "jakaś liczba" do potęgi 8
29 paź 11:41
dawsonika: no ale ta liczba na , ktora zamienie 4 musi byc rowna 4 np. a8= 4 , czyli musze znac
pierwiastek 8 stopnia z 4 ?
29 paź 11:43
Tadeusz:
x
8>4 ⇒ x
8−4>0 ⇒ (x
4−2)(x
4+2)>0 ⇒ (x
2−
√2)(x
2+
√2)(x
4+2)>0
itd
29 paź 11:44
Tadeusz:
Ty rozwiązujesz nierówność a nie równanie
Szukasz przedziałów a nie jednego pierwiastka
29 paź 11:45
dawsonika: czyli bede miec 3 wyniki ? x1= √2 x2=−√2 x3=−2?
29 paź 11:46
dawsonika: wiec jedyne rozwiazanie bedzie x1 bo jest 0>0 i rozne od 1
29 paź 11:46
J:
Ty masz zdawać maturę w tym roku ?
29 paź 11:47
J:
jeżeli: A*b*c > 0 i wiemy,że: b >0 i c > 0 , to wniosek: A jest ?
29 paź 11:49
dawsonika: A >0 . Juz zdalem ale zapomnialem jak sie robi tego typu zadanie
29 paź 11:50
J:
no to lecisz.... x2 − √2 > 0
29 paź 11:51
dawsonika: no wlasnie jesli uzyje wzory a2−b2 = (a−b)(a+b) to wychodzi na to ,ze zamiast √2 mam wpisac
√ 4 stopnia z 2 ?
29 paź 11:55
J:
tak
29 paź 11:56
dawsonika: to bedzie : (x−4√2)(x+4√2) ⇒x1= 4√2 ,x2= −4√2
29 paź 11:58
dawsonika: x4+2 jak rozlozyc ,zrobic ? nie ma wzoru a2+b2
29 paź 11:59
J:
a po co masz to rozkładać ?
29 paź 12:00
dawsonika: czyli do ostatecznego wyniku zaliczymy jedynie x=4√2 , uwzgledniajac dziedzine ?
29 paź 12:02
J:
oprzytomniej ... masz wyznaczyć te wartości x, dla których trójmian kwadratowy: x2 − √2
przyjmuje warości dodatnie
29 paź 12:03
Tadeusz:
pisałem ... PRZEDZIAŁY
29 paź 12:04
dawsonika: czyli : (−∞;−4√2)∪(4√2;∞) ?
29 paź 12:12
J:
teraz skonfrontuj to z założeniem
29 paź 12:13
dawsonika: Z: x>0 i x≠1 ⇒ x∊(4√2;∞) ?
29 paź 12:17
J:
popatrz 11:35
29 paź 12:22
dawsonika: x∊(4;∞) dla x (0;1) ?
29 paź 12:35
dawsonika: pogubilem sie troche ztym tam jest napisane 4<x8 a x8 ∊ do przedzialu z 12;12
29 paź 12:38
J:
przecież dla: x ∊ (0,1) masz nierówność: x8 − √2 < 0
29 paź 12:39
dawsonika: 11;35 napisales za dla x∊(0,1) 4>x8 a nie x8−√2
29 paź 12:42
dawsonika: wogle nigdzie nie mielismy takiej postaci ,ze bylo x8−√2
29 paź 12:43
J:
człowieku .. to jest precież ta sama parabola:
x8 − 4 > 0 ( juz rozwiązałeś ) , teraz: x8 − 4 < 0 ... i rozwiązuj
29 paź 12:45
dawsonika: x8−4<0 ⇒ x∊(−4√2;4√2) ?
29 paź 12:47
J:
czyli teraz rozwiązujesz: x2 − √2 < 0
29 paź 12:48
J:
dobra ..., ale teraz znowu skonfrontuj z załozeniem: x ∊ (0,1)
29 paź 12:49
dawsonika: przedzial (−4√2;4√2) skonfrotnowac z przedzialem (0,1) czy tamto zostaje a teraz rozwiazuje
x2−√2 <0 i wynik tego konfrontuje z zalozeniem ?
29 paź 13:00
J:
tamto zostaje .. teraz rozwiązujesz x2 − √2 , 0 i x ∊ (0,1)
rozwiązaniem zadania jest suma: to co juz masz plus to co dostaniesz teraz
29 paź 13:03
Eta:
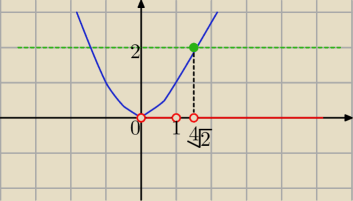
Z wykresu:
f(x)= x
8
y=2
dla x>1 4<x
8 ⇔ x
8>4 ⇔ x
4>2 ⇔
x>4√2
dla x∊(0,1) 4>x
8 ⇔ x
8<4 ⇔ x
4<2 ⇔ x∊(−
∞,
4√2) i x∊(0,1) ⇒
x∊(0,1)
Odp :
x∊(0,1) U (4√2,∞)
29 paź 13:03
Eta:
Oczywiście wykres f(x) = x4
29 paź 13:06