Funkcja logarytmiczna
ambitny18: Określ dziedzinę funkcji f i naszkicuj jej wykres.
Witam, kompletnie nie rozumiem tego zadania, siedzę nad nim drugi dzień, proszę o szczegółowe
wytłumaczenie

Ten przykład udało mi się rozwiązać− ale nie rozumiem dlaczego dla x ∊ ( 0;1) => f(x) = −1,
więc o ten przykład również proszę.
A najtrudniejsze jest to..
Proszę o najbardziej jak to możliwe przejrzyste wytłumaczenie, naprawdę chcę to zrozumieć. Z
góry bardzo dziękuję
28 paź 21:06
ambitny18: Zerknie ktoś? <zdesperowany>
28 paź 21:16
ambitny18: <Bliski płaczu..>

28 paź 21:29
Mati15:
To powinno pomóc

28 paź 21:32
ambitny18: A jednak nie pomogło..
28 paź 21:35
Mati15: wolframalpha.com

28 paź 21:39
Mila:
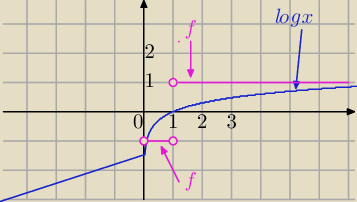
Zadanie 1)
Zał. x>0 i logx≠0⇔x≠1i x>0
a)
|logx|=logx dla logx>0 ⇔x>1
Wtedy
| | logx | |
f(x)= |
| =1⇔f(x)=1 dla x>1 |
| | logx | |
b)
|logx|=−logx dla x∊(0,1) wtedy :
f(x)=−1 dla x∊(0,1)
28 paź 23:40
Mila:
Program , sfałszował, to odgałęzienie z III ćwiartki ma" iść" w dół
28 paź 23:43
wszechpotrzebujacy: Jakbyś mi adres podała, to wysłałbym Ci kwiaty... Dziękuję bardzo, że Ci się chciało, nie
pomyślałem, aby dołożyć do tego wykres f. log.
Jeju, jestem naprawdę wdzięczny!
28 paź 23:44
Eta:
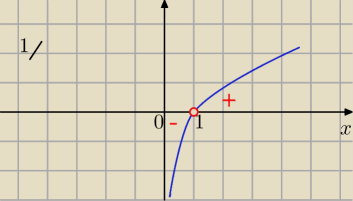
1/ y=logx −−−− patrz wykres (1)
|logx|= + logx dla x>1
− logx dla x∊(0,1)
| | logx | |
f(x)= |
| = 1 dla x>1 |
| | logx | |
| | logx | |
f(x)= |
| = −1 dla x∊(0,1) |
| | −logx | |
| | logx | |
teraz narysuj wykres 2/ f(x)= |
| |
| | |logx| | |
28 paź 23:46
Mila:
2) poradzisz sobie?
28 paź 23:46
wszechpotrzebujacy: Mam nadzieję, że jeszcze któraś z przemiłych Pań posiedzi, spróbuję drugi zrobić!

28 paź 23:47
Eta:
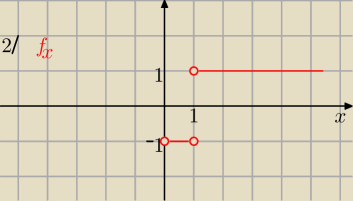
28 paź 23:48
wszechpotrzebujacy: A posiedzi, że w sensie do ewentualnego skorygowania błędów.

28 paź 23:48
Eta:
No i masz babo placek .......... jak ja to "kocham"

28 paź 23:48
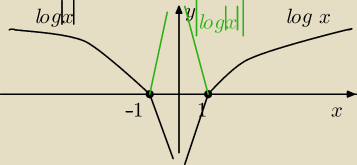
Eta:
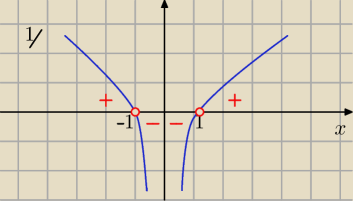 y
y= log|x|
28 paź 23:59
Eta:
| | log|x| | |
f(x)= |
| =1 dla x ∊( −∞, −1) U (1,∞) |
| | log|x| | |
| | −log|x| | |
f(x)= |
| = −1 dla x∊(−1,0) U (0,1) |
| | log|x| | |
29 paź 00:04
wszechpotrzebujacy: Własnie byłem w trakcie robienia tego przekładu, ale nie wiedziałem ile rozważyć przypadków.
Dlaczego nie rozpatrujesz przypadku
itd..
PS. Za wszystko bardzo dziękuję, ten łatwy przykład jarzę w 100%

29 paź 00:19
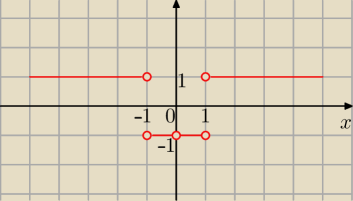
wszechpotrzebujacy:
Eta, a Twój wykres 1 do drugiego zadania nie powinien wyglądać tak? Przepraszam za ten wykres,
nie wiem jak wy to tak ładnie rysujecie. ...
29 paź 00:33
Eta:
Ja na tym wykresie zaznaczyłam Ci wartości dodatnie i ujemne
stąd "puste" kółeczka ... i jeszcze puste w zerze ( zaznacz)
29 paź 00:55
wszechpotrzebujacy: Prawie zrozumiałem już wszystko, tylko mam pytanie. Ta moja funkcja narysowana na moim rysunku,
ta zielona, czyli załóżmy, że mamy f(x)= |log|x|| to dziedzina takiej funkcji to wszystkie
liczby oprócz zera czy wszystkie liczby oprócz {−1,0,1} ? Skoro x musi być większe od 0, to
będzie chyba ten drugi zbiór, prawda?
29 paź 01:10
wszechpotrzebujacy: Pytanie powyższe odnośni się TYLKO odnośnie dziedziny funkcji f(x)= |log|x|
29 paź 01:10
wszechpotrzebujacy: f(x)= |log|x|| * oczywiście dwa moduły
29 paź 01:13
olejnik: Dziedziną f(x)= |log|x|| są wszystkie liczby oprócz zera.
29 paź 01:21




 Zadanie 1)
Zał. x>0 i logx≠0⇔x≠1i x>0
a)
|logx|=logx dla logx>0 ⇔x>1
Wtedy
Zadanie 1)
Zał. x>0 i logx≠0⇔x≠1i x>0
a)
|logx|=logx dla logx>0 ⇔x>1
Wtedy
 1/ y=logx −−−− patrz wykres (1)
|logx|= + logx dla x>1
− logx dla x∊(0,1)
1/ y=logx −−−− patrz wykres (1)
|logx|= + logx dla x>1
− logx dla x∊(0,1)




 y= log|x|
y= log|x|


 Eta, a Twój wykres 1 do drugiego zadania nie powinien wyglądać tak? Przepraszam za ten wykres,
nie wiem jak wy to tak ładnie rysujecie. ...
Eta, a Twój wykres 1 do drugiego zadania nie powinien wyglądać tak? Przepraszam za ten wykres,
nie wiem jak wy to tak ładnie rysujecie. ...