sieczna i styczna
olla:
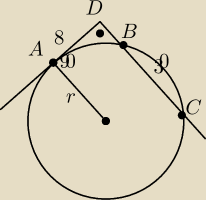
Styczna do okręgu i sieczna są wzajemnie prostopadłe. Punkty A jest punktem styczności prostej
i okręgu, punkty B i C punktami wspólnymi siecznej i okręgu, punkt D punktem wspólnym stycznej
i siecznej. AD=8 BC=30 zadanie z gimnzajum
27 paź 22:59
Janek191:
Jakie jest pytanie ?
27 paź 23:05
olla: Jaki jest promień ?
27 paź 23:06
Janek191:
r2 = 82 + 152 = 64 + 225 = 289
r = 17
27 paź 23:06
Janek191:
Pitagoras
27 paź 23:07
olla: skąd 15 ?
27 paź 23:07
olla: pitagoras to kombinowałam, ale skąd 15 ?
27 paź 23:07
Janek191:
30 : 2 = 15
27 paź 23:10
Janek191:
Połącz środek okręgu z punktem B i środkiem cięciwy BC. Masz Δ prostokątny
27 paź 23:11
olla: Pitagorasa kombinowałam w tym trójkącie powinno być 82 + (302+DB2)=AC2 i potem dumałam co
dalej? ale już wiem,że nie tam trzeba było zbudować trójkąt − dzięki.
27 paź 23:15
Janek191:
27 paź 23:21
Eta:
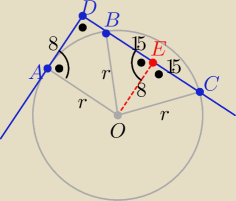
Nie podajesz co masz obliczyć ? zapewne długość promienia "r" tego okręgu
Jeżeli gimnazjum to:
trapez AOCD jest prostokątny o wysokości |AD|= |OE|=8
bo trójkąt COB jest równoramienny o ramionach długości "r"
Z twierdzenia Pitagorasa w trójkącie OEB
r
2=15
2+8
2 ⇒ r=
√289= 17
27 paź 23:21
Eta:
Oooo .... już
Janek rzucił się na "karmę"
27 paź 23:23
Janek191:
I Eta również
27 paź 23:25
Eta:
27 paź 23:25