Zadanie nr 1.23 5-latek: Zadanie Zbadaj wzajemne polozenie okregow o(A,r₁) i o(B,r₂) w zaleznosci od parametry m jeśli a) |AB|=3m+1 r₁= m−2 r₂= 2m+3 b) |AB|= 0,5m−3 r₁= 0,75m +1 r₂= 0,25m+1 c) |AB|=5m−4 r₁= 2m+1 r₂= m−3 zrobiłem a) r₁+r₂= 3m+1 wiec r₁+r₂=|AB| wiec okręgi te będą stycznie zewnętrznie dla m>2 bo dla m=1 i m=2 okrag o(A,r₁) nie istnieje wb) r₁+r₂= m+2 > |AB| ale tu posilbym o pomoc

Eta: https://matematykaszkolna.pl/strona/473.html

5-latek: Dobry wieczor Eta Ja to mam przed sobą z książki Tak teraz patrze ze okrag o(B,r₂) będzie się zawieral w okręgu o(A,r₁) wiec będą to okręgi rozlaczne wewnwnetrzie bo |AB|<|0,75m+1−0,25m+1| Tylko teraz jak wyznaczyć to m

kyrtap: 5− latku do spania

5-latek: Czesc Zaraz wlasnie ide

Mila: Dobranoc, jutro napiszę

5-latek: Dobrze Milu Dobranoc

Mila:

	1
b) |AB|=		m−3 gdzie m≥6
	2

r₁+r₂=m+2

	1
|r1−r2|=		m
	2

1) a) m=6 okręgi współśrodkowe b) kiedy r₁+r₂<|AB| (okręgi rozłączne zewnętrznie)

	1
m+2<		m−3 i m>6
	2

1
	m<−5⇔m<−5 i m>6 brak rozwiązania
2

c) r₁+r₂=|AB| brak rozwiązania d) |r₁−r₂|<|AB|<r₁+r₂| ( przecinające się)⇔

1		1
	m<		m−3 <m+2
2		2

	1
0<−3 (sprzeczność) i −		m<5 brak
	2

e) |AB|=|r₁−r₂| styczne wewnętrznie

1		1
	m−3 =		m
2		2

−3=0 sprzeczność brak rozwiązania f) |AB|<|r₁−r₂| rozłączne wewnętrznie

1		1
	m−3<		m i m>6
2		2

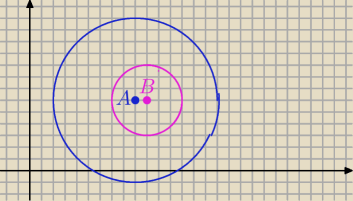
−3<0 i m>6⇔m>6 Rysunek: m=8

	1
|AB|=		*8−3=1
	2

r₁=7 r₂=3

5-latek: Dobry wieczor Milu Pozdrawiam dziekuje Ci bardzo

Mila: witam.

Mila: (c) zrobione?

5-latek: Milu zrobie