rozwiazac nierownosc knykieckowski:

1		1
	≥
|x+3|		|x−6|

===: ... dlaczego pomimo, że to nierówność mogę "na krzyż" |x−6|≥|x+3| itd

knykieckowski: jak już to |x−6|≤|x+3|

knykieckowski: tylko nie ogarniam dalej bo wychodzą mi sprzeczne w różnych przypadkach

misiak:

	1		1
własność: 0<a<b ⇔		>
	a		b

misiak: czyli: |x+3≤|x−6|

knykieckowski: no tak napisałem to, chodzi mi o dalsze rozwiązanie zadania, nigdy nie ogarniałem bezwzględnej

misiak: napisałeś z przeciwnym zwrotem nierówności

misiak: |x+3≤|x−6| (x+3)²≤(x−6)² 6x+9≤−12x+36 18x≤27

	3
x≤
	2

Aga1.: Zaczynamy od założeń x≠−3 i x≠6 wtedy Ix+3I>0 i Ix−6I>0 , mnożymy przez wspólny mianownik, a nie jak to często bywa przez mianownik do kwadratu.

knykieckowski:

	3
niestety w odp jest inaczej, x≤		jest złą odp, więc podnoszenie tych 2 stron do kwadratu
	2

jest również błędną metodą, pozdrawiam

misiak: a jaką podano odpowiedź? i jaka to książka?

misiak: metoda w tym wypadku jest prawidłowa

===: ...daj sobie z nim spokój ... szkoda czasu i atłasu Ten typ tak ma

knykieckowski:

	3
x∊(−∞;−3) u (−3;		>
	2

nie wiem jaka to książka, mam tylko zadania i odp. do nich, które są wzięte z jakiejś książki

misiak: po uwzględnieniu założeń : x≠−3 i x≠6 otrzymujemy tę właśnie odpowiedź

	3
x∊(−∞,		) \ {−3}
	2

misiak:

	3
poprawka: x∊(−∞,		>\{−3}
	2

knykieckowski: yyy panie === nie chcesz nie pomagaj, buraku

knykieckowski: a fakt dzięki misiak

===: a potrafisz "złożyć" x≠−3 i x≤3/2

===: ... i co prostaczku knykieckowski ... słoma i buractwo wychodzi Metoda zła bo twoja wiedza = ZERO

Eta: 1 sposób algebraicznie Na wstępie założenia : x≠ 6 , x≠ −3

	3
|x−6|≥|x+3| |2 ⇔ x2−12x+36≥ x2+6x+9 ⇔ 18x≤27 ⇔ x≤		i x≠ −3
	2

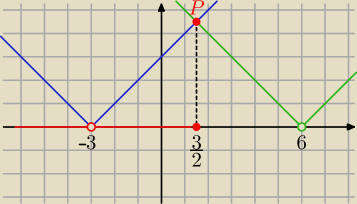
odp: x∊(−∞, ³₂> \ {−3} 2sposób graficznie rysujemy wykresy f(x)= |x−6| i g(x)=|x+3| i uwzględniamy założenia wykresy przecinają się w punkcie P o odciętej x_P

	3
x−6= −x−3 ⇒ 2x= 3 ⇒ xP=
	2

Odp: x∊(−∞, ³₂> \{−3}

Eta: Oooo ... gdybym wiedziała ,że jesteś taki arogancki to dostałbyś zero rozwiązania !