Wyznacz największą liczbę całkowitą spełniającą nierówn2^x - U{7}{4} < U{1}{4^x} K: Wyznacz największą liczbę całkowitą spełniającą nierówność :

	7		1
2x −		<
	4		4x

moje rachunki:

	7		1		1
2x −		<		<		2x=t , t>0
	4		4x		22x

	7		1
t −		<		/ *t2
	4		t2

	7
t3 −		t2 < 1
	4

	7
t2 ( t −		) < 1
	4

i nie wiem co dalej .. ;<

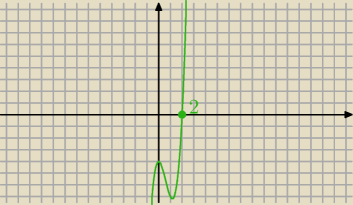
J: To jest wykres: 4t³ − 7t² − 4

K: Dzięki, ale chciałbym wiedzieć jak to algebraicznie rozwiązać.

J: jak każą nierówność trzeciego stopnia ... odgadujemy ,ze: x = 2 jest pierwiastkiem, potem dzielisz wielomian przez dwumian : x − 2

K: dobra, wyliczyłem sobie pierwiastek z tego za pomocą wzrou x=p/q . z wcześniejszej postaci, gdzei były ułamki coś nie mogłem wyliczyć.