#A1
RJS:
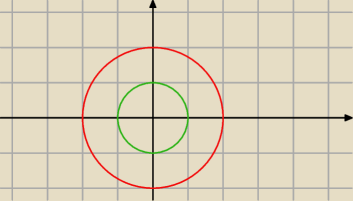
A=x
2+y
2<1
B=x
2+y
2<4
A∪B=B ?
26 paź 02:49
RJS:
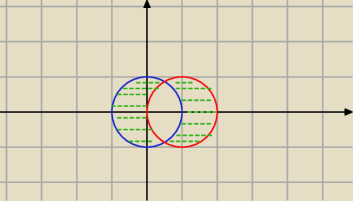
B) A∪C
A=x
2+y
2<1
C=(x−1)
2+y
2<1
26 paź 02:53
J:
A) OK
B) źle ... suma wnętrz obydwu kół
( suma zbiorów to ogół elementów, które należą do A lub należą do C )
26 paź 06:05
RJS:
Ale to nie będzie cześć wspólna ?
26 paź 17:51
52: Nie
26 paź 17:56
RJS:
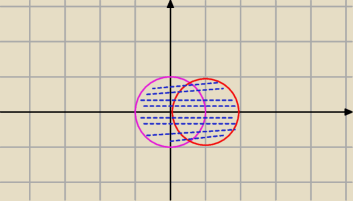
Czyli ?
A∪C =?
26 paź 18:04
52: no to właśnie, tylko jak to zapisać ?
26 paź 18:11
RJS:
Hmm, nie wiem
26 paź 18:16
RJS:
..
26 paź 20:22
RJS:
halp
26 paź 20:59
RJS:
:(
26 paź 21:16
Kacper:
A∪C={(x,y)∊R2: x2+y2<1 ∨ (x−1)2+y2<1}
26 paź 21:37
RJS:
Kacper pomożesz jeszcze ?
26 paź 21:59
RJS:
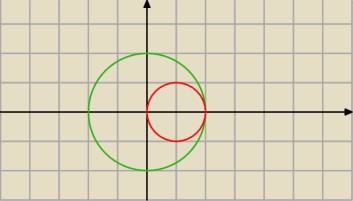
B∪C=B ?
B=x
2+y
2<4
C=(x−1)
2+y
2<1
26 paź 22:05
RJS: ...
26 paź 22:45
Eta:
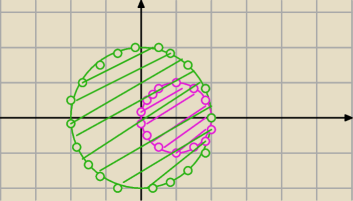B U
C=
B
26 paź 23:54
RJS:
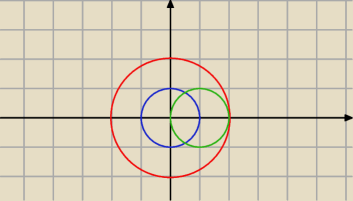
AUBUC ?=A
A=x
2+y
2<1
B=x
2+y
2<4
C=(x−1)
2+y
2<1
27 paź 00:01
RJS:
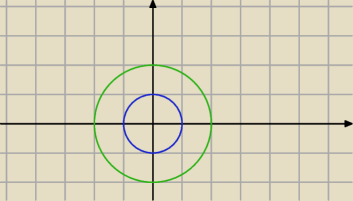
A=x
2=y
2<1
B=x
2+y
2<4
A∩B=A ?
27 paź 00:02
RJS:
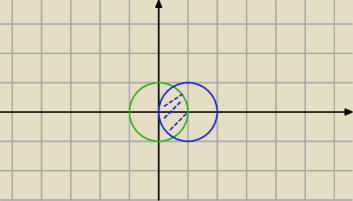
A=x
2+y
2<1
C=(x−1)
2+y
2<1
A∩C= jak opisać tą łezkę ?
27 paź 00:03
Eta:
ok
27 paź 00:04
RJS: A post 00:03 ?
27 paź 00:23
RJS:
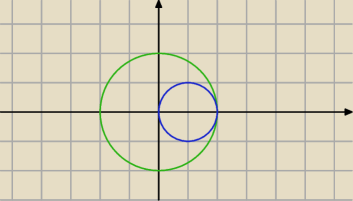
B=x
2+y
2<4
C=(x−1)
2+y
2<1
B∩C=C
27 paź 00:24
Eta:
A∩B={(x,y): x,y∊R ⋀ x2+y2<1 ⋀ (x−1)2+y2<1}
27 paź 00:25
RJS:
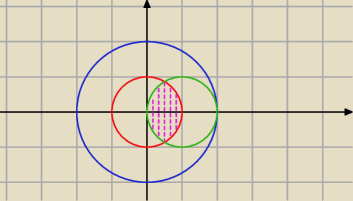
A∩B∩C
A=x
2+y
2<1
B=x
2+y
2<4
C=(x−1)
2+y
2<1
i znowu ta łezka ?
27 paź 00:25
RJS:
Eta mały lapsu u Ciebie A∩C winno być
27 paź 00:26
RJS:
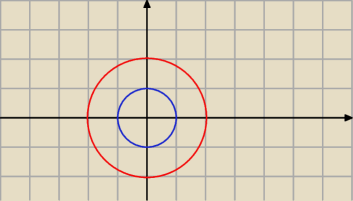
A\B=∅
A=x
2+y
2<1
B=x
2+y
2<4
27 paź 00:29
Eta:
koniunkcja trzech nierówności
27 paź 00:30
RJS:
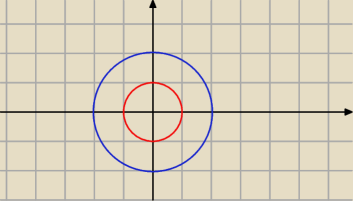
B\A=x
2+y
2=1 ?
A=x
2+y
2<1
B=x
2+y
2<4
27 paź 00:30
Eta: 00:29 ok
27 paź 00:31
RJS:
00:25
to będzie takie coś ?
x2+y2<1 ⋀ (x−1)2+y2<1
27 paź 00:33
Eta:
Niebieski pierścień z czerwonym brzegiem
27 paź 00:34
Eta:
00:25 jeszcze trzecia nierówność (bo koniunkcja trzech
27 paź 00:36
RJS:
00:25 nie wiem jak
27 paź 00:36
Eta:
A∩B∩C= = {(x,y) x,y∊R ⋀x2+y2<1 ⋀ (x−1)2+y2<1 ⋀ x2+y2<4}
27 paź 00:39
RJS:
00:30 jest ok ?
27 paź 00:39
Eta:
Odp do 00:30 jest mój wpis o 00:34
( pierścień bez niebieskiego brzegu z czerwonym brzegiem
27 paź 00:46
RJS:
x2+y2<4 ⋀x2+y2=1 ?
27 paź 00:47
RJS:
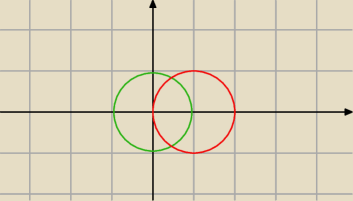
i ostatnie
A=x
2+y
2<1
C=(x−1)
2+y
2<1
A\C=x
2+y
2<1 − (x
2+y
2<1 ∧(x−1)
2+y
2<1) ?
27 paź 00:49
Eta:
x2+y2<4 ⋀ x2+y2≥1
27 paź 00:49
Eta:
00:49
x2+y2<4 ⋀ (x−1)2+y2≥1
27 paź 00:52
RJS:
00:49 jest ok ? (Mój post) ?
27 paź 00:52
RJS:
Dziękuję Ci bardzo za pomoc ! Oby więcej takich ludzi to maturkę R zdam na 100 %
(marzenia)
27 paź 00:53
Eta:
Nie odp: w moim wpisie 00:52
27 paź 00:54
Eta:
Dasz radę
27 paź 00:55