wyznacz okres podstawowy funkcji olga: wyznacz okres podstawowy funkcji y = |sin x| + |cos x|

PW: f(x) = |sinx| + |cosx| Tego nie umiem, ale umiem wyznaczyć okres funkcji f²(x)

olga: jak?

misiak:

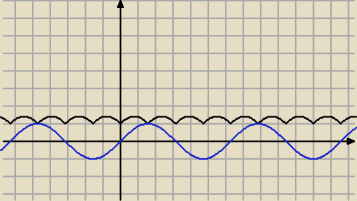
	π
rysunek podpowiada, że będzie to
	2

misiak: f(x)=|sinx|+|cosx|

	π		π
f(x+t)=|sin(x+		)|+|cos(x+		)|=|cosx|+|−sinx|=|cosx|+|sinx|
	2		2

trzeba by jeszcze pokazać, że to najmniejsza liczba o tej własności

PW: Tak, jak rysunek zrobiła maszyna. Uczeń na egzaminie nie ma takiej możliwości. Pomyśl, olgo, ile to jest (|sinx|+|cosx|)²

olga: 1 + 2|sin x cos x|?

PW: A gdy "wciągniesz dwójkę między kreski" to ...

olga: 1 + | sin 2x |

olga: i wtedy jest okres podstawowy ^π₂?

PW: No i mamy

	π
f2(x) ma okres
	2

Czy znamy okres f(x)?

olga: taki sam?

misiak: y=sinx ma okres 2π y=sin²x ma okres π

olga: to ja już nie rozumiem...

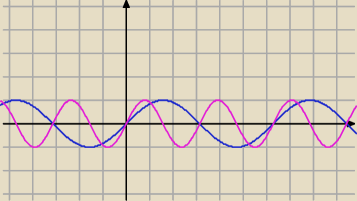
misiak: wygląda na to, że nie można tak uogólniać

olga: w takim razie jaki będzie okres mojego f(x)?

misiak:

	π
jest równy
	2

olga: czyli z tego że moje f²(x) ma okres ^π₂ wynika to, że f(x) ma taki sam czy nie? no bo wtedy po prostu te "brzuszki" będą niższe, tak?

PW:

	π
Skoro wartości f2(x) powtarzają się co		, to wartości √f2(x) = |f(x)| też powtarzają
	2

	π
się co		. W tym wypadku √f2(x) = f(x), bo funkcja f(x) jest z definicji nieujemna.
	2

misiak, nie mąć w głowie, nic nie "uogólniałem". Powtarzam: nie trzeba przy takich dowodach posługiwać się wykresami, które rysuje program.