Oblicz objętość stożka i ostrosłupa. Roksana: Zadanie 1. Oblicz wysokosc stozka, ktorego powierzchnia boczna jest wycinkiem koła o kącia środkowym 300 stopni i tworzącej dlugosci 12. Zadanie 2. Oblicz długość krótszej przekątnej graniastosłupa prawidłowego sześciokątnego, którego wysokosc wynosi 10, a krawędz podstawy ma długosc 6. Oblicz cosinus kąta nachylenia tej przekatnej do podstawy. Zadanie 3. Wysokość ściany bocznej ostrosłupa prawidłowego trójkątnego wynosi 6 i jest nachylona do plaszczyzny podstawy pod kątem 30 stopni. Oblicz objętość tego ostrosłupa. Zadanie 4. Przekątna przekroju osiowego walca jest nachylona do podstawy pod kątem α, takim ze tgα=²₃. Promien podstawy walca ma glugosc 24. Wyznacz objętosc walca.

olekturbo: tak mało zadań

Roksana: Hehe, pomogloby mi, gdybym miala chociaż jedno zadanie. Naprawdę będę wdzięczna za każdą pomoc

olekturbo: α = 60 l = 12

h
	= sin60
l

h = 6√3

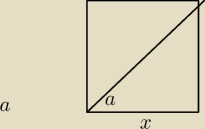
olekturbo: x = 2r x = 48 tga = 2/3 h/x = 2/3 h/48 = 2/3 h = 32 v = π576*32 = 18432π

Roksana: a mógłbys mi jeszcze wytłumaczyć w pierwszym zadaniu skąd wzięło się α=60? Dziękuję za szybkie odpowiedzi

sushi_gg6397228: cyrkiel i nożyczki do ręki rysujesz okrąg, zaznaczasz sobie kąt środkowy 300 i wycinasz składasz i masz stożek

Roksana: Kurczę, przepraszam za kłopot, ale czy ktoś mógłby mi narysowac i objaśnić jeszcze raz zadanie pierwsze? Bo wiadomo, mogłabym tylko przepisać, ale chciałabym również zrozumieć...

sushi_gg6397228: wykonaj polecenie z 21.55

Roksana: A da sie to jakoś wyliczyc matematycznie?

sushi_gg6397228: jak wytniesz sobie, to zobaczysz do jest promieniem w dużym kole, co wycinkiem łuku a co r i l i obwodem podstawy stożka

sushi_gg6397228: masz r=12 liczysz wycinek łuku ł = 20π stąd r= 10

Roksana: Dobrze, doszłam juz do tego, jak wyliczyć że r równe jest 10. Ale licząc dalej, próbowałam z pitagorasa. Jak mam juz l i r wyliczylam h i wyszło mi 2√11 a nie 6√3, tak jak to wyszło olkowiturbo

Roksana: bo próbowalam w ten sposób : h² + 10² = 12² h² = 44 h= 2√11

Roksana:

sushi_gg6397228: a czy miało wyjsc tak samo czy masz kąt α = 60 ^o ?

Roksana: teraz mi wyszło jeszcze całkowicie inaczej. poszperałam troche w internecie i zrobilam wszystko analogicznie do zadania 10 http://matematyka.opracowania.pl/gimnazjum/sto%C5%BCek/ l=12 α=300 Pb = ¹₃ πl² Pb = ¹₃ π* 144 Pb = 48 π cm² Pb= πrl 48π = πr12 / 12π r=4 i teraz z pitagorasa h² +r²=l² h² +16=144 h²=128 h= √128 h=4√8

Roksana: Pomyłka, zrobilam to inaczej, promien wyszedł 10, wysokość nadal 2 pierwiastki z 11. Oto jak: Pb= ³⁰⁰₃₆₀*πl² Pb = ⁵₆*144π =120π Teraz zabrałam sie za wyliczenie promienia r. ³⁰⁰₃₆₀*2πl=2πr r=⁵₆ *12 = 10 Czyli tak jak wam r wyszło mi 10. I dalej... h²=l²−r² h= 2√11