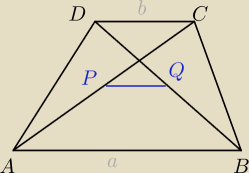
. xoxo: niech punkty P i Q bedą srodkami przekatnych trapezu ABCD. oblicz dł odc PQ znając dł podstaw trapezu

pigor: ..., z warunków zadania, tw. o odcinkach łączących środki kolejnych boków ΔΔ i a>b jak na rys, to masz np. równanie: ¹₂a − |PQ| = ¹₂b ⇒ |PQ|= ¹₂(a − b) i a>b . ...

xoxo: a mógłbys napisac o jakie dokładnie twierdzenie Ci chodzi..bo takiego nie kojarze

xoxo: chodzi ci o linie która łaczy srodki dówch boków trójkąta,.?...tylko ze w tym przypadku ja tego tak nie widze,..

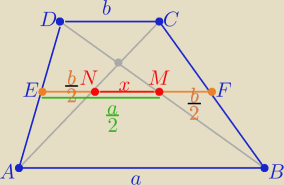
Eta: Z podobieństwa trójkątów w skali k=2

	a		b
ABD ∼ EMD |EM|=		oraz ΔBCD ∼ΔBMF to |MF|=|EN|=
	2		2

	a		b		a−b
x=		−		=
	2		2		2

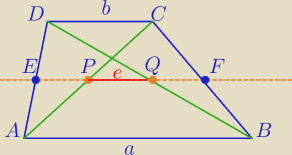
Mila: Rozpisuję dokładnie:

	1
|PF|=		a jako odcinek łączący środki boków ΔABC
	2

	1
|QF|=		b jako odcinek łączący środki boków ΔDCB
	2

	1		1
e+		b==		a
	2		2

	a−b
e=
	2

xoxo: dziękuje Wam baardzo

xoxo: do tego rysunku jest jeszcz jedno zadanie: niech A,B,C,D bedzie dwolnym trapezem o danych podstawach. załóżmy, że P i Q są punktami leżącymi odpowiednio między A i C oraz B i D takimi , że S(A,C; P)=S(B,D; Q)=λ wyraź dł odc. PQ jako funkcę zmiennej λ

xoxo: czyli mozna zapisać tak: ze S(A,C; P)=|AP|\|CP| ? a S(B,D; Q)=|BQ|\|DQ| ..dalej nie wiem co robic