znajdź m karko: Pewnie było pierdyliard razy. Określ liczbę rozwiązań w zależności od m.

x2+4x+1
	=m
x2+1

Czy mogę zignorować mianownik i zrobić równanie x²+4x+1=0 wyliczyć deltę, wyliczyć q i określić m jako m=q i m>q ?

sushi_gg6397228: to juz bylo z tydzień temu, poszukaj na forum

karko: oks

olekturbo: Przeprowadź przebieg zmienności funkcji i sprawdź, kiedy y = m przecina wykres funkcji

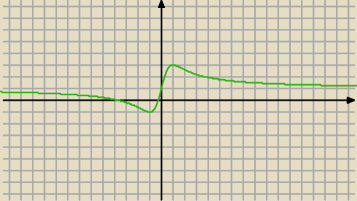
ax: ... widzisz dlaczego nie ... ?

Kacper: olek nie potrzeba strzelać z armat o kaczek

Mila: x²+4x+1=m*(x²+1)⇔ x²+4x+1=mx²+m x²−mx²+4x+1−m=0 (1−m)*x²+4x+1−m=0 1) 1−m=0 ⇔m=1 to mamy równanie liniowe: 4x+1−1=0 4x=0 x=0 jedno rozwiązanie: 2) 1−m≠0 mamy równanie kwadratowe a) Δ=0 jedno rozwiązanie Δ=16−4*(1−m)*(1−m)⇔ 4(1−m)²=16 (1−m)²=4 1−m=2 lub 1−m=−2 m=−1 lub m=3 lub b) Δ>0 16−4(1−m)²>0 [4−2(1−m)]*[4+2*(1−m)]>0 (4−2+2m)*(4+2−2m)>0 (2+2m)*(6−2m)>0 (2*(1+m)*2(3−m)>0 m∊(−1,3) dwa rozwiązania c)Δ<0⇔m<−1 lub m>3 brak rozwiązan.

daras: pierdyliard+1 raz