okrag opisany na trojkacie brzoza: Na okręgu o promieniu 4 opisano trójkąt prostokątny o jednej z przyprostokątnych długości 10.Oblicz długości pozostałych boków.

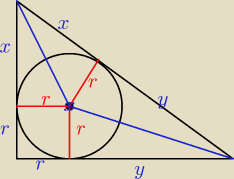
Basia: x+r=10 x+4=10 x=6 (x+r)²+(y+r)²=(x+y)² 10²+(y+4)²=(6+y)² 100 + y²+8y+16=36+2y+y² 6y = −80 y = − ⁸⁰₆ niemożliwe; y>0 (dłigość odcinka) zadanie nie ma rozwiązania

Maciek: Jak to nie ma rozwiązania? Długości boków: a = 10 b = 24 c = 26 10²+24²=26²

Basia: a policz promień okręgu wpisanego w ten trójkąt

Basia: sinα=¹⁰₂₆ = ⁵₁₃

	a		10
R =		=		=13
	2sinα		1013

a w zadaniu jest R=4

Bogdan:

	1
r =		(a + b − c)
	2

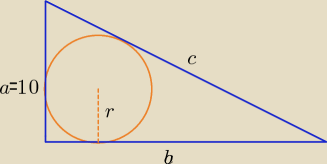
	1
4 =		(10 + b − c) ⇒ 8 = 10 + b − c ⇒ c − b = 2
	2

Z tw. Pitagorasa: c² − b² = 100 ⇒ (c − b)(c + b) = 100 ⇒ 2*(c + b) = 100 c − b = 2 c + b = 50 2c = 52 ⇒ c = 26 i b = 24

Basia: Masz rację Bogdanie. Pomyliłam wzory. Ale proszę znajdź błąd w moim pierwszym rozwiązaniu, bo za diabła go nie widzę.

Basia: No jasne "1" zjadłam, a potem już poszło 10²+(y+4)²=(6+y)² 100 + y²+8y+16=36+12y+y² −4y = −80 y=20 a=10 b=20+4=24 c=6+20=26

Niepewny: Na okręgu o promieniu 4 opisano trójkąt prostokątny o jednej z przyprostokątnych długości 10.Oblicz długości pozostałych boków r=4 a=10 c=a√2 c=20 b=a√3 b=10√3