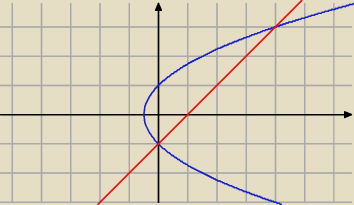
obszar RJS: Mam obliczyć pole ograniczone funkcjami y²=2x+1⇒y=√2x+1 y=−√2x+1 y=x−1 ∫(√2x+1−x+1)dx=∫√2x+1dx−∫xdx+∫dx

	1		1
=		√(2x+1)3−		x2+x+C
	3		2

	14		16
po podstawieniu granic całkowania wyszło mi		w odpowiedzi jest
	3		3

RJS: Czy granice całkowania do od 4 do 0 ?

J: Nie możesz tak całkować, bo w przedziale [0,4] funkcja "niebieska" się zmienia .. zmień kolejność całkowania

RJS: W przedziale od 4−0 przecież niebieska ogranicza z góry cały czas ?

J: sorry ... źle popatrzyłem ... musisz mieć bład w obliczeniach , bo granice są dobre [0,4]

RJS: Mam tak (pomijam na razie granice całkowania ) ∫(√2x+1−x+1)dx=∫√2x+1dx−∫xdx+∫dx=....

	1
∫√2x+1dx=		√(2x+1)3+C
	3

	1		1
..=		√(2x+1)3−		x2+x+C
	3		2

Wstawiam teraz granice całkowania

	1		1		1		14
[		√(2x+1)3−		x2+x]=5−		=
	3		2		3		3

Więc gdzie się mylę ?

J: policzyłem ... i masz dobrze

Godzio: Jeżeli koniecznie chcesz tak całkować to: P = ∫_−1/2⁰(√2x + 1 − (−√2x + 1))dx + ∫₀⁴(√2x + 1 − (x − 1))dx A można też po y całkować i wtedy:

	y2 − 1
P = ∫−13(y + 1 −		)dy
	2

J: zaćmienie .. no jasne: granice to: [−1/2,4] i zmiana funkcji podcałkowych

RJS: Godzio ten czubek od −1/2 do 0 też należy do obszaru ? w tym punkcie przecież nie ogranicza go prosta y=x−1 ?

RJS: Nie było pytanie, mnie też zaćmiło Dziękuję Panowie !

Godzio: Prosta może nie, ale y² = 2x + 1 już tak.