|sinx| + sinx = 0 lipstone1: |sinx| + sinx = 0 sinx = sinx lub sinx = −sinx x należy do rzeczywistych lub x=kπ ale powinno wyjść x należy <π+2kπ,2π+2kπ> Mógłby ktoś wytłumaczyć?

olekturbo: założenia: dla sinx ≥ 0 sinx = −sinx dla sinx <0 sinx = sinx

ICSP: albo zastanowic się kiedy równanie : a + |a| = 0 ma rozwiązania i w jakiej postaci są te rozwiazania.

lipstone1: no dobra, z pierwszego założenia wychodzi że x = π+2kπ. To skąd 2π+2kπ?

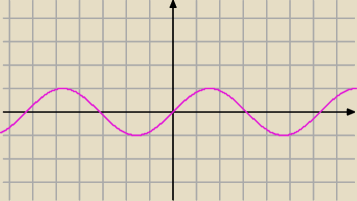
Aga1.: Gdy sinx<0 czyli.x∊(π+2kπ,2π+2kπ) mamy −sinx+sinx=0 0=0 odp x∊(π+2kπ, 2π+2kπ) gdy sinx≥0, czyli x∊<0+2kπ, π+2kπ> mamy sinx+sinx=0 2sinx=0 sinx=0 x=kπ należy do dziedziny. odp x∊(π+2kπ,2π+2kπ)U{kπ}= odp z książki.

lipstone1: aaaaaa dobra. Dzięki bardzo