Wartość bezwzględna - sposób rozwiązania
Tup: Witam. Mam pytanie: Czy mój sposób rozwiązywania równości z dwiema wartościami bezwzględnymi
jest poprawny? Robię to tak:
1. Wyznaczam 4 warianty w których opuszczę wartości bezwzględne ( na przykładzie ):
a) dwa moduły są ≥ 0
b) dwa moduły są < 0
c) pierwszy moduł ≥ 0 drugi <0
d) pierwszy moduł <0 drugi ≥0
( z definicji wartości bezwzględnej )
Następnie wyznaczam przedziały, do których x musi należeć no i liczę. Jestem ciekaw czy aby na
pewno dobrze to rozumiem.
Pozdrawiam
przykład:
http://imgur.com/jOCmq1t
Mila:
|3x+6|−|3−x|=−1 możemy zapisać tak:
(1)
|3x+6|−|x−3|=−1
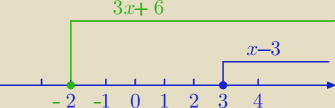
1) |3x+6|=3x+6 dla x≥−2
2) |x−3|=x−3 dla x≥3
zaznaczam na os i liczbowej:
Rozważam w przedziałach:
a)x<−2 wtedy równanie (1) ma postać:
−3x−6−(−x+3)=−1⇔−3x−6+x−3=−1⇔−2x=8
x=−4∊D
b) x∊<−2,3)
3x+6−(−x+3)=−1
4x=−4
x=−1∊D
c) x≥3
3x+6−(x−3)=−1
2x+6+3=−1
2x=−10∉<3,
∞)
Może tak będzie Ci łatwiej.
I przede wszystkim krócej, dziękuje 