Funkcja wykładnicza XpomocyX: Może ktoś mi pomóc z tym zadaniem? Dla jakich wartości parametru m, gdzie m∊R − {−1,1}, równanie 3/ [(1/3)^x + (1/3)²x + (1/3)³x +...] = (2−m)/(m²−1) ma rozwiązanie? Bardzo proszę o pomoc

XpomocyX: Równanie to: 3/ [(1/3)^x + (1/3)^2x + (1/3)^3x +...] = (2−m)/(m²−1)

Tadeusz: popatrz co masz w mianowniku

XpomocyX: Zaczęłam tak: a₁= (1/3)^x q=(1/3)^x ozn: (1/3)^x=t i t>0 S= t/ (1−t) Dlatego: 3/ [t/ (1−t)] = (3−3t)/t i dalej nie wiem co zrobić...

Tadeusz: ... chyba jednak błędna ścieżka ... dla x<0

XpomocyX: Czyli to co zrobiłam jest źle?

XpomocyX: Jeszcze założenie, ze |g|<1 czyli |(1/3)^x|<1 (1/3)^x<1 i (1/3)^x>−1 dlatego x∊(0, +nieskończoności)?

Tadeusz: narysuj wykres "lewej strony" i "tnij" prawą otrzymasz

2−m
	>0
m2−1

XpomocyX: narysowałam wykres (3−3t)/t, ale nie rozumiem o co chodzi z tym cięciem, możesz mi to wytłumaczyć? Po obliczeniu (2−m)/(m²−1)>0 wynik wychodzi prawidłowy jednak chciałabym zrozumieć cięcie prawej strony

XpomocyX: i dlaczego (2−m)/(m²−1)>0? Bo tego nie rozumiem...

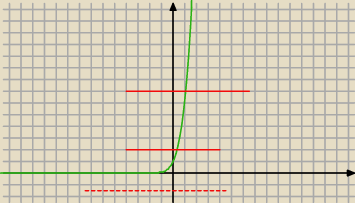
Tadeusz: Wyrażenie w mianowniku przyjmuje wartości (∞, 0) zatem cała lewa strona (0, ∞)

XpomocyX: dlaczego mianownik przyjmuje wartości <0? W mianowniku jest t, a postawiłam założenie, że t>0 − czy ono jest błędne? i czy to jest wykres (3−3t)/t? bo mnie wyszedł inaczej...

===: Noc to zły czas na myślenie. 1. Pozostaw już to swoje (3−3t)/t 2. Ja też błędnie zapisałem przedział dla mianownika Twego podstawowego równania ... powinno być (0,∞)

===: przeanalizuj:

3
3−x+3−2x+3−3x+...

− jest ciągła − lim x→−∞ 0 − lim x→ ∞ ∞ − ZW=(0,∞) czyli y∊R: y>0 Jeśli ma zachodzić:

3		2−m		2−m
	=		to		>0
3−x+3−2x+3−3x+...		m2−1		m2−1

XpomocyX: Wielkie dzięki za pomoc i cierpliwość!

Tadeusz: