liczby zespolone
demi: Korzystając z interpretacji geometrycznej modułu różnicy liczb zespolonych wyznaczyć i
narysować
zbiory liczb zespolonych spełniających podane warunki:
| z2+4z−2i |≤5 probowalam podstawic za z=x+iy i podniesc do kwadratu a pozniej opuscic
modul ale wychodza pozniej bardzo duze potegi i nie wiem co z tym zrobic.
21 paź 19:23
PW: Gdybyś napisała ułamek używając wielkiej litery "U", to byłoby czytelne.
21 paź 19:37
21 paź 19:43
21 paź 19:45
Mila:
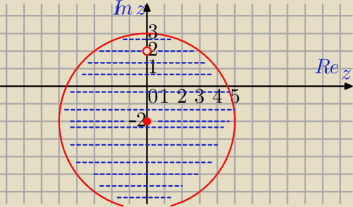
z≠2i
|z
2+4|≤5*|z−2i|⇔
|z
2−4i
2|≤5|z−2i|⇔
|z−2i|*|z+2i|−5|z−2i|≤0⇔
|z−2i|*(|z+2i|−5)≤0⇔
|z−2i|>0 z def. modułu, zatem
|z+2i|≤5
Koło o środku (0,−2) i r=5 bez punktu (0,2).
21 paź 20:13
Benny: Czy możemy zrobić tak?
|z+2i|≤5
21 paź 20:15
demi: nie rozumiem ostatnich linijek
|z−2i|>0 z def. modułu, zatem
|z+2i|≤5
21 paź 20:30
Mila:
Kiedy iloczyn dwóch liczb jest ujemny?
a*b<0
a>0 i b<0
lub a<0 i b>0
w zadaniu wychodzi, że :
(|z+2i|−5)≤0⇔
|z+2i|≤5
21 paź 20:47
demi: okey dzieki

21 paź 20:54
demi: (i−2)
24(13+9i)
8 mam jeszcze takie zadanie z gwiazdka i tez cos mi nie wychodzi:
|z|=
√5
a w tablicach nie odczytam takiego kata ? moze jakas podpowiedz
21 paź 21:14
demi: (i−2)24(13+9i)8
21 paź 21:15
Mila:
Zaraz przeliczę.
21 paź 21:18
Mila:
[(i−2)
3]
8*(13+9i)
8=
=(11i−2)
8*(13+9i)
8=
=[−125+125i]
8
|z|=|−125+125i|=125
√2
Punkt; (−125,125)
| | 3π | | 3π | |
z8=(125√2)8*[cos( |
| *8)+i sin( |
| *8)] |
| | 4 | | 4 | |
z
8=(5
3)
8*2
4*[cos(6π)+i sin(6π)]=
=5
24*2
4*[1+0]=2
4*5
24
21 paź 21:39
demi: dzieki wielkie

21 paź 21:59
Mila:
No to zbieraj jutro punkty na ćwiczeniach.
21 paź 22:03
 z≠2i
|z2+4|≤5*|z−2i|⇔
|z2−4i2|≤5|z−2i|⇔
|z−2i|*|z+2i|−5|z−2i|≤0⇔
|z−2i|*(|z+2i|−5)≤0⇔
|z−2i|>0 z def. modułu, zatem
|z+2i|≤5
Koło o środku (0,−2) i r=5 bez punktu (0,2).
z≠2i
|z2+4|≤5*|z−2i|⇔
|z2−4i2|≤5|z−2i|⇔
|z−2i|*|z+2i|−5|z−2i|≤0⇔
|z−2i|*(|z+2i|−5)≤0⇔
|z−2i|>0 z def. modułu, zatem
|z+2i|≤5
Koło o środku (0,−2) i r=5 bez punktu (0,2).

