L. zespolone. Theosh: Liczby zespolone Potrafi ktoć obliczyć pierwiastek 4 stopnia z −4 + 4i?

Mila: Potrafi, a Ty jaką masz propozycję? ⁴√−4+4i=√2*⁴√−1+i Co dalej potrafisz?

Theosh: skąd wziełaś √2 ? przecież moduł do 4√2 ?

Theosh: nie mam kompletnie pomysłów u nas pani inaczej rozpisywała na wykładzie.

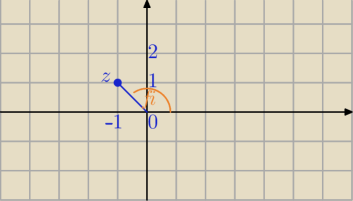
Mila: To tylko pierwsze przekształcenie, abyś łatwo odczytał argument. ⁴√−4+4i=⁴√4*(−1+i)=⁴√4*⁴√(−1+i) ⁴√4=⁴√2²=√2 z'=−1+i możesz teraz łatwo odczytać argument

	3π
φ=
	4

to do wzorów de Moivre'a, czy tak liczyliście, czy podstawialiście : ⁴√−4+4i=x+iy, gdzie x,y∊R |z|=|−4+4i|= √4²+4²=√32

Theosh: Wychodzą mi jakieś kosmiczne wyniki np:

	3		3
4√{32}(cos		+ isin		) czy tak w ogóle powinno być
	16		16

Theosh: ?

Mila: Błędy w zapisie :

	3π		3π		3π		3π
z0=4√√32*[ cos		+i sin		]=8√32*[ cos		+i sin		]
	16		16		16		16

Niestety takie wyniki, trzeba pomyśleć nad ułatwieniem. Masz odpowiedź do zadania?

Theosh: niestety nie. ale pani mówiła, że w każdym będą "ładne liczby". skoro załapałem to to pomożesz mi zaczać z innym zadaniem z liczb zespolonych? Bardzo krótkie.

Theosh: z⁴+5z²+4=0

Mila: Tak.

Mila: Może w tym poprzednim masz inne liczby pod pierwiastkiem ⁴√... ? 23:15 rozwiązuj jak normalne równanie dwukwadratowe.

Theosh: "dla dlicz z zadania 2 oblicz podane liczby: ⁴√z" a w zadaniu 2 z=−4 +4i

Theosh: czyli np. t=z² i moje równanie wygląda wtedy t²+5t+4?

Mila: z²=v v²+5v+4=0 Δ=9 v₁=−4 lub v₂=−1 z²=−4 lub z²=−1 z²+4=0 lub z²+1=0 ( skorzystamy z tego, że i²=−1) z²−4i²=0 lub z²−i²=0 (z−2i)*(z+2i)=0 lub (z−i)*(z+i)=0 z=2i lub z=2i lub z=i lub z=−i

Theosh: Milu kłaniam Ci się po pas

Mila:

daras: raczej w pas

daras: jopas