funkcja kwadratowa_parametry patrycja: Wyznacz te wartości parametru k, dla których równanie (k+1)x² −2x + k − 1 = 0 ma dwa różne rozwiązania należące do przedziału (0; 2). W rozwiązaniu wyszło mi, że k∊ (−√2, −1) suma (1, √2). Jednak w odpowiedziach zbiór podaje tylko odpowiedzi dodatnie, czyli k∊ (1, √2). Czy może mi ktoś wytłumaczyć, dlaczego rozwiązania ujemne nie wchodzą w grę? Pozdrawiam i z góry dziękuję za poświęcony mi czas. undefined

Bogdan: Jakie przyjęłaś założenia?

Tadeusz:

	2
xw=
	k+1

	2
0<		<2 i stąd między innymi ...
	k+1

PW: Wskazówka: Pomyśl o pierwszej współrzędnej wierzchołka paraboli (warto posługiwać się ilustracjami).

J: 1) Δ > 0 2) 0 < x_w < 2 3) Dla: k+1 > 0 f(0) > 0 i f(2) > 0 Dla: k+1 < 0 f(0) < 0 i f(2) < 0

pigor: ..., proponuję taką koniunkcję (układ) nierówności (warunków) : f(x)=ax²+bx+c=0 i α< x₁< x₂< β ⇔ Δ>0 i a*f(α)>0 i a*f(β)>0 i α<x_w<β.

J: ładnie uproszczony mój 3) warunek

pigor: ..., racja, bo załatwia jednakowe znaki współczynnika "a" i wartości f(.). ...

patrycja: No jasne, ale już chyba z założenia f(0)>0 i jednocześnie f(2)>0 (przy opcji, że k+1>0) (i analogicznie przy k+1<0) wynika, że odcięta wierzchołka paraboli będzie należeć do przedziału (0,2) Skoro pierwiastki są pomiędzy 0 i 2 to chyba logiczne, że tym bardziej wierzchołek jest pomiędzy tymi liczbami. Czy muszę dodatkowo wprowadzać takie założenie?

Tadeusz: narysuj ... a zobaczysz

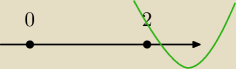
J: nie masz racji ... popatrz

patrycja: Ok, teraz już rozumiem i właśnie o to mi chodziło. Zadań tego typu jest od groma i do dobrego ich rozwiązania potrzebne jest właściwe zrozumienie zawartych w nich założeń. Dziękuję i pozdrawiam