a izii: Sześcian przecięto płaszczyzną przechodzącą przez przekątną dolnej podstawy oraz środki dwóch krawędzi górnej podstawy . Pole otrzymanego przekroju wynosi 40,5 cm². Oblicz objętość tego sześcianu. Wykonałem rysunek : http://imgur.com/LQqWayT Tylko co dalej ?

izii:

irena_1: Z pierwszego rysunku: a− długość krawędzi sześcianu |A₂C₁|=a√2

	a√2
|E1F1|=
	2

	a		a2		5
|F1C1|2=a2+(		)2=a2+		=		a2
	2		4		4

	ap%]
|F1C1|=
	2

Z drugiego rysunku (trapezu): |FG|=h |AC|=a√2

	a√2
|EF|=
	2

	a√5
|FC|=
	2

	a√2
|GC|=
	4

	a√2		a√5
h2+(		)2=(		)2
	4		2

	5		2		20−2		18
h2=		a2−		a2=		a2=		a2
	4		16		16		16

	3√2
h=		a
	4

	a√2+a√22		3√2		3√2a		3√2		9
P=		*		a=		*		a=		a2
	2		4		4		4		8

9		81
	a2=40,5=
8		2

a²=36 a=6cm V=a³ V=216cm³

irena_1:

	a√5
|F1C1|=
	2

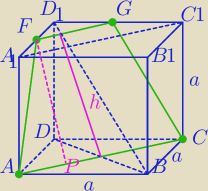Mila: |AC|=A₁C₁|=a√2

	1		a√2
|FG|=		|AC|=
	2		2

	a√2+√22
PACGF=		*h
	2

	a√2+√22
40.5=		*h /*2
	2

	3a√2
81=		*h
	2

162=3a√2*h

	1
|AP|=(a√2−		a√2):2
	2

	a√2
|AP|=
	4

|AP|²+h²=|AF|²

	a		5
|AF|2=a2+(		)2=		a2
	2		4

	a√2		5
(		)2+h2=		a2
	4		4

2		20
	a2+h2=		a2
16		16

	18		9
h2=		a2=		a2
	16		8

	3a
h=
	2√2

	3a
162=3a√2*
	2√2

	9a2
162=
	2

324=9a² a²=9 a=6 V=6³=216 ===========