okrąg - trapez
ewa: Na okręgu opisano trapez równoramienny ABCD (|AB|=a, |CD|=b).
a) Oblicz długość ramienia trapezu
b) Oblicz długość wysokości trapezu
c)Wykaż, że pole trapezu jest nie mniejsze niż kwadrat długości wysokości
d) Wykaż, że średnia harmoniczna długości podstaw w tym trapezie jest nie większa niż średnia
geometryczna ich długości.
| | 2 | |
(Średnia geometryczna liczb a i b to √ab, śrdnia harmoniczna to |
| ) |
| | | |
9 gru 20:07
ewa: 
9 gru 22:09
ewa: a przy tym by mi ktos pomogl

bardzo prosze
10 gru 00:16
Basia: Pomogę
10 gru 00:21
ewa: naprawde jestem bardzo wdzieczna

!
10 gru 00:23
Basia:
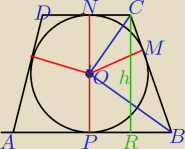
tr.ONC i OMC są przystające ⇒ |CM| = |NC| =
b2
tr.OPB i OMB są przystające ⇒ |BM| = |BP| =
a2
|BC|=|AD| = |BM|+|CM| =
a+b2
|RB| =
a−b2
h
2+|RB|
2 = |BC|2
h
2 = (
a+b2)
2−(
a−b2)
2
| | a2+2ab+b2−a2+2ab−b2 | | 4ab | |
h2 = |
| = |
| |
| | 4 | | 4 | |
h
2=ab
h=
√ab
P =
a+b2*h =
a+b2*
√ab
mamy pokazać, że P≥h
2 ⇔
a+b2*
√ab≥ab
przypuśćmy, że jest odwrotnie czyli, że
a+b2*
√ab<ab /*2
(a+b)*
√ab<2ab podnosimy obustronnie do kwadratu
(a+b)
2*ab<4a
2b
2 /:ab
(a+b)
2<4ab
a
2+2ab+ b
2<4ab
a
2−2ab+b
2<0
(a−b)
2<0
sprzeczność, czyli przypuszczenie jest fałszywe czyli
a+b2*
√ab≥ab
czyli
P≥h
2
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
ad.d
nie tylko w tym trapezie;
to jest prawdą dla każdych dwóch liczb dodatnich
udowodnić tak samo jak z polem i wysokością
10 gru 00:47
magda: nie rozumiem tego d jak rozwiazać pomoże ktos


?
28 gru 12:10
magda: 

?
29 gru 10:02
magda: czyli z tym polem i wysokoscia nie musze robic odwrotnosci.. i na koniec wychodzi wynik
(a−b)
2 ≥ 0 i mozna to w ten sposob zrobic i juz zostawic

29 gru 18:52
magda: 

29 gru 19:19

 bardzo prosze
bardzo prosze
 !
!
 tr.ONC i OMC są przystające ⇒ |CM| = |NC| = b2
tr.OPB i OMB są przystające ⇒ |BM| = |BP| = a2
|BC|=|AD| = |BM|+|CM| = a+b2
|RB| = a−b2
h2+|RB|2 = |BC|2
h2 = (a+b2)2−(a−b2)2
tr.ONC i OMC są przystające ⇒ |CM| = |NC| = b2
tr.OPB i OMB są przystające ⇒ |BM| = |BP| = a2
|BC|=|AD| = |BM|+|CM| = a+b2
|RB| = a−b2
h2+|RB|2 = |BC|2
h2 = (a+b2)2−(a−b2)2

 ?
?

 ?
?


