nierownosci liczby zespolone
Bogdan: Czesc
moze mi ktos wytlumaczyc jak postepowac z takimi nierownosciami w liczbach zespolonych:
|z−2i | / |z+3| <1, z∊ℂ
Rozpisalem to tak :
|z −3i | < | z+3|
No i teraz co dalej? Podnsic do kwadratu czy jak?
Na plaszczyznie zespolonej oznacza to tyle, ze odleglosc od punktu z (3i) musi byc mniejsza niz
odleglosc od punktu z (−3).
20 paź 16:43
J:
to narysuj symetralną odcinka o końcach: z1 = − 2 oraz z2 = 3i
i zastanów się ,które punkty spełniają tą nierówność
20 paź 16:48
J:
z1 = − 3 oczywiście
20 paź 16:48
J:
no ... w treści jest :I z − 2i I , czyli: z1 = − 3, z2 = 2i
20 paź 17:00
Bogdan:
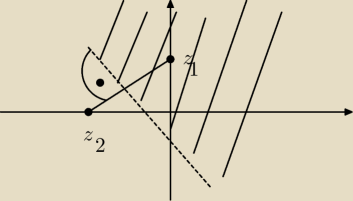
Tak ma wygladac ten przedzial? Bo w wolframie pokazuje mi to co zakreskowalem ale wylacnie w 3
i 4 cwiertce. Dlaczego?
20 paź 17:17
Bogdan: Poprawka, nawet inaczej pokazuje w tej 3 i 4 cwiartce niz to co tutaj mam
20 paź 17:18
Bogdan: Wie ktos gdzie jest ta roznica?

20 paź 19:38
Mila:
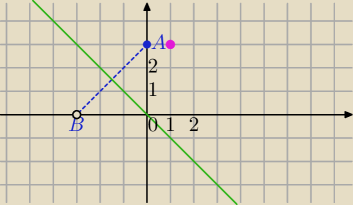
Zbiór punktów spełniających równanie: |z −3i | = | z+3| to symetralna odcinka AB :
|z−(0+3i)|=|z−(−3+0i)|
A=(0,3) i B=(−3,0)
P(x,y) − punkt symetralnej (symetralna to zbiór punktów jednakowo odległych od końców odcinka
AB)
(x−0)
2+(y−3)
2=(x+3)
2+(y−0)
2
x
2+y
2−6y+9=x
2+6x+9+y
2
−6y=6x
y=−x
Taka nierówność :
|z −3i | < | z+3| oznacza zbiór punktów na jednej z półpłaszczyzn.
Łatwo ustalisz wybierając punkt np.( 1,3)) i podstawiasz do nierówności
z
0=1+3i
L=|1+3i−3i|=1
P=|1+3i+3|=|4+3i|=
√16+9=5
1<5 zatem wybierasz półpłaszczyznę na symetralną.
20 paź 20:47
Mila:
Możesz dojść do tego algebraicznie:
|z −3i | < | z+3|
z=x+iy
|x+iy−3i|<|x+iy+3|⇔
|x+i*(y−3)|<|(x+3)+iy|
p{x2+(y−3)2<(x+3)2+y2⇔
x2+y2−6y+9<x2+6x+9+y2⇔
−6y<6x
y>−x punkty nad prostą y=−x bez punktów na prostej
20 paź 20:52
 Tak ma wygladac ten przedzial? Bo w wolframie pokazuje mi to co zakreskowalem ale wylacnie w 3
i 4 cwiertce. Dlaczego?
Tak ma wygladac ten przedzial? Bo w wolframie pokazuje mi to co zakreskowalem ale wylacnie w 3
i 4 cwiertce. Dlaczego?

 Zbiór punktów spełniających równanie: |z −3i | = | z+3| to symetralna odcinka AB :
|z−(0+3i)|=|z−(−3+0i)|
A=(0,3) i B=(−3,0)
P(x,y) − punkt symetralnej (symetralna to zbiór punktów jednakowo odległych od końców odcinka
AB)
(x−0)2+(y−3)2=(x+3)2+(y−0)2
x2+y2−6y+9=x2+6x+9+y2
−6y=6x
y=−x
Taka nierówność :
|z −3i | < | z+3| oznacza zbiór punktów na jednej z półpłaszczyzn.
Łatwo ustalisz wybierając punkt np.( 1,3)) i podstawiasz do nierówności
z0=1+3i
L=|1+3i−3i|=1
P=|1+3i+3|=|4+3i|=√16+9=5
1<5 zatem wybierasz półpłaszczyznę na symetralną.
Zbiór punktów spełniających równanie: |z −3i | = | z+3| to symetralna odcinka AB :
|z−(0+3i)|=|z−(−3+0i)|
A=(0,3) i B=(−3,0)
P(x,y) − punkt symetralnej (symetralna to zbiór punktów jednakowo odległych od końców odcinka
AB)
(x−0)2+(y−3)2=(x+3)2+(y−0)2
x2+y2−6y+9=x2+6x+9+y2
−6y=6x
y=−x
Taka nierówność :
|z −3i | < | z+3| oznacza zbiór punktów na jednej z półpłaszczyzn.
Łatwo ustalisz wybierając punkt np.( 1,3)) i podstawiasz do nierówności
z0=1+3i
L=|1+3i−3i|=1
P=|1+3i+3|=|4+3i|=√16+9=5
1<5 zatem wybierasz półpłaszczyznę na symetralną.