Rachunek prawdopodobieństwa - 2 łatwe zadania :) Szymon: Ktoś tu jeszcze nie śpi? prosze o pomoc Zad. 1 Rzucamy dwa razy sześcienną kostką, na której ściankach znajdują się następujące liczby oczek: 1, 2, 3, 4, 6, 6. Prawdopodobieństwo tego, że suma wyrzuconych oczek jest większa od 10, jest równe: A. 1/4 B. 1/6 C. 1/9 D. 1/12 Zad. 2 Niech A,B ∈ Ω. Oblicz P (A\B) , jeśli: P(B) = 1/2 i P(A∨B) = 3/4

Qulka: C

Qulka: 3/4−1/2 =1/4

Szymon: Okej , dzięki a mogłabyś mi Qulka jeszcze rozpisać, w jaki sposób wyszedł Ci wynik 1/9 w zad. 1 ? z jakiego wzoru korzystałaś w zad. 2?

Qulka: bo większe od 10 jest tylko 12 więc 2•2=4 ze wszystkich możliwych 6•6=36 w drugim z logiki wszystko co jest w A i nie jest w B to od sumy AUB odejmuję B jak podzielę obustronnie przez Ω to mam pr−wo

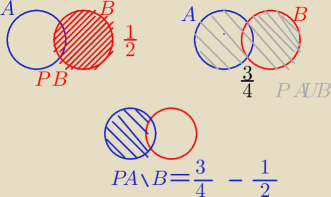yht: Zad. 1 Aby suma oczek była większa od 10, to za pierwszym razem musisz wyrzucić 6 i za drugim razem musisz wyrzucić 6 prawdopodobieństwo wyrzucenia 6 w pojedynczym rzucie wynosi 1/3, zaś spójnik i odpowiada za mnożenie, więc wynik to 1/3 * 1/3 = 1/9 Zad. 2 Wzory to P(A\B)=P(A)−P(A∩B) oraz P(A∪B)=P(A)+P(B)−P(A∩B) Wstawiasz pierwszy wzór do drugiego i masz P(A∪B)=P(B)+P(A\B)

3		1		1
	=		+P(A\B) → P(A\B)=
4		2		4

Jednak zdecydowanie się rozjaśni jeśli rozrysujesz to na zbiorach (rys. na samym początku) − od zamalowanych obu kółek A i B odejmujesz B i dostajesz zbiór A\B czyli to co należy do A ale nie należy do B

Szymon: Baaaardzo dziękuję za pomoc