Da się bez pochodnej? qqaazzxx: Czy da się obliczyć minimum dla √x²−12x+37+√x²−2x+17 bez użycia pochodnej? A jeśli nie to moglibyście rozwiązać to z pochodną? (W szkole niby jeszcze nie miałem, coś na kółku było ale nie dużo, wiem tylko ze bochodna pierwiastka to 1/2pierwiastki * (pochodna tego co jest pod pierwiastkiem) więc proszę o pomoc w liczeniu ekstrem

Qulka: pod pierwiastkiem parabole więc minimum pod pierwiastkiem to min suma dwóch najmniejszych da min całości (na szczęście pierwiastki są tylko dodatnie

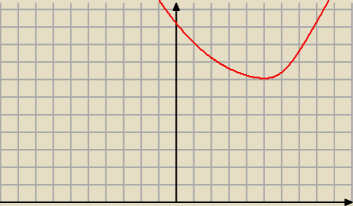
b.: Można się spodziewać, że f(x)= √(x−6)²+1 + √(x−1)²+16 ma minimum w x=5. Nie widzę, jak to pokazać, ale na pewno się da bez pochodnych.

b.: @Qulka: nie, to nie jest poprawne rozumowanie.

olekturbo: Troche jednak zle rozumiesz pochodne bo to pochodna złożona

b.: @olekturbo: przecież napisał, że ,, * (pochodna tego co jest pod pierwiastkiem) ''

olekturbo: ale jeszcze * pochodna funkcji wewnetrznej

b.: no ale ta funkcja wewnętrzna to właśnie ,,to co jest pod pierwiastkiem''

olekturbo:

	1
hm bo jego wpis zrozumialem jako		tylko bez 2x−12
	2√pierwiastek

w takim razie Dobranoc

Qulka: no tak..to muszą być te same x

RJS: Qulka zobaczy moje zadanko ?

qqaazzxx: To mógłby ktoś to rozwiązać? To trzeba rozwiazac f(x)'=0 i w tych punktach beda ekstrema?

Qulka: tak

daras: minimum dla x = 5