a izii: Dla akich wartości parametru a równanie |x−2|=a²−3a−2 ma dwa pierwiastki różnych znaków ?

olekturbo: narysuj sobie y = |x−2| i sprawdz kiedy ma dwa pierwiastki roznych znakow

izii: Ale jak sprwdzic kiedy ma 2 pierwiastki roznych znakow ?

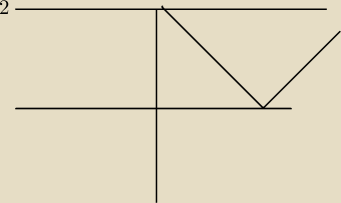
olekturbo: y = |x−2| ma dwa pierwiastki roznych znakow gdy jest wieksze od 2 a²−3a−2 > 2 a²−3a−4 > 0 Δ = 9 + 16 = 25 i lecimy

pigor: ..., ponieważ, L(x)=|x−2|| i L(0)= |0−2|= |−2|= −(−2)= 2, to warunki zadania spełnia nierówność P(a)=a²−3a−2 >2 ⇔ a²−3a−4 >0 ⇔ ⇔ (a−4)(a+1) >0 ⇔ a<−1 v a>4 ⇔ a∊(−∞;−1) U (4;+∞) .

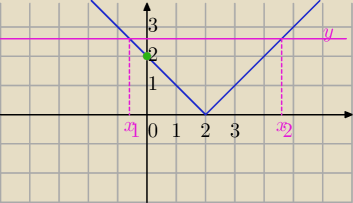
Mila: prosta na rysunku przecina wykres w dwóch punktach, gdzie x₁<0 i x₂>0 Zatem masz dwa rozwiązania o różnych znakach dla y=a²−3a−2 >2 rozwiąż:

izii: A jeżeli będę chciał obliczyć dla jakiego a równanie ma dwa pierwiastki tych samych znaków/dwa pierwiastki dodatnie/dwa pierwiastki ujemne ?

olekturbo: tych samych znakow x ∊ (0,2)

izii: A dwa dodatnie ?

olekturbo: dwa dodatnie tak samo dwoch ujemnych nie moze byc

izii: Równanie a(x+1)+x=b(x−1)+5 gdzie x jest niewiadomą ma nieskończenie wiele rozwiązań. Znajdź liczby a i b.

pigor: ..., np. tak: a(x+1)+x=b(x−1)+5 ⇔ ax+a+x=bx−b+5 ⇔ (a−b+1)x= −a−b +5 ma ∞ wiele rozwiązań ⇔ a−b+1=0 i −a−b+5=0 /+ stronami ⇔ ⇔ −2b+6= 0 i a−b+1= 0 ⇔ b=3 i a=2 ⇔ (a,b)=(2,3) . ...