 Na okręgu o promieniu r opisano trapez równoramienny ABCD (AB>CD). Punkt styczności S dzieli
Na okręgu o promieniu r opisano trapez równoramienny ABCD (AB>CD). Punkt styczności S dzieli
| |CS| | 2 | |||
ramię trapezu tak, że | = | . Wyznacz długość ramienia oraz długość przekątnej | ||
| |SB| | 5 |



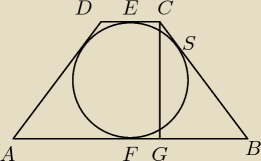 Szkic rozwiązania:
Oznaczam: |CS| = 2x, |SB| = 5x, wtedy jest spełniony warunek |CS||SB|=25
wtedy |CB| = 7x
Z własności stycznej |CS| = |CE| czyli |CD| = 4x oraz |SB|=|FB| czyli |AB| = 10x
a stąd |GB| = 3x
teraz tw. Pitagorasa dla trójkąta CGB: (2r)2 + (3x)2 = (7x)2
skąd wyliczamy x i następnie |CB|
|AC| obliczysz teraz z tw. Pitagorasa dla trójkąta AGC.
Szkic rozwiązania:
Oznaczam: |CS| = 2x, |SB| = 5x, wtedy jest spełniony warunek |CS||SB|=25
wtedy |CB| = 7x
Z własności stycznej |CS| = |CE| czyli |CD| = 4x oraz |SB|=|FB| czyli |AB| = 10x
a stąd |GB| = 3x
teraz tw. Pitagorasa dla trójkąta CGB: (2r)2 + (3x)2 = (7x)2
skąd wyliczamy x i następnie |CB|
|AC| obliczysz teraz z tw. Pitagorasa dla trójkąta AGC.
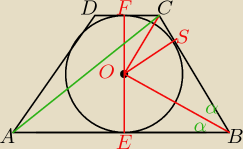 tr. BEO i BSO są przystające ⇒ BE = BS
tr. CFO o CSO są przystające ⇒ FC = CS
tr. BSO i OSC są podobne
tr. BEO i BSO są przystające ⇒ BE = BS
tr. CFO o CSO są przystające ⇒ FC = CS
tr. BSO i OSC są podobne
| BS | OS | ||
= | |||
| SO | SC |
| BS | r | ||
= | |||
| r | SC |
| CS | 2 | ||
= | |||
| SB | 5 |
| 2 | ||
CS = | *SB | |
| 5 |
| 2 | ||
r2 = | *|BS|2 | |
| 5 |
| √5*r | √10r | |||
|BS| = | = | |||
| √2 | 2 |
| √10r | ||
|CS| = | ||
| 5 |
| √10r | √10r | |||
BC = | + | = | ||
| 2 | 5 |
| 7√10r | |
| 10 |
| √10r | ||
|BE|=|BS| = | ||
| 2 |
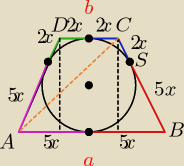 b=4x
a=10x
b=4x
a=10x
| 10x−4x | ||
(2r)2 + ( | )2 = (7x)2
| |
| 2 |
| r | r√10 | |||
x= | = | |||
| √10 | 10 |
| r√10 | r√10 | 2r√10 | 5r√10 | 7r√10 | ||||||
2* | + 5* | = | + | = | ||||||
| 10 | 10 | 10 | 10 | 10 |
| r√10 | ||
4r2 +49( | )2=e2
| |
| 10 |
| 49r2 | ||
4r2 + | =e2
| |
| 10 |
| 89r2 | |
=e2
| |
| 10 |
| r√890 | ||
e= | ||
| 10 |
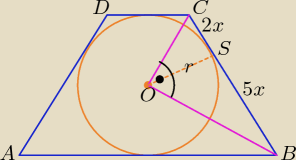 Dobry wieczór.
x > 0, r > 0
Dobry wieczór.
x > 0, r > 0
| 2x | r | |||
Z podobieństwa trójkątów CSO i SOB otrzymujemy proporcję: | = | . | ||
| r | 5x |
| r | ||
Stąd 10x2 = r2 ⇒ √10 x = r ⇒ x = | . | |
| √10 |
| 7r | ||
Długość ramienia |BC| = 2x + 5x = 7x = | ||
| √10 |
 któy to
jest odcinek w tym trójkacie
któy to
jest odcinek w tym trójkacie
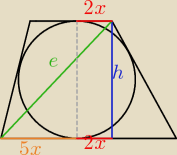 e2=(7x)2 +h2 gdzie h=2r
e2=(7x)2 +h2 gdzie h=2r
 i |AD|2+|DC|2=|AC|2
gdzie |AD| = 7x
|AC|= e
|DC|= wg ciebie 2r i dlaczego tak jest
i |AD|2+|DC|2=|AC|2
gdzie |AD| = 7x
|AC|= e
|DC|= wg ciebie 2r i dlaczego tak jest bo tego wlasnie nie rozumiem
bo tego wlasnie nie rozumiem
 DZIEKUJE WSZYSTKIM ZA POMOC
DZIEKUJE WSZYSTKIM ZA POMOC