Matura RJS: Jak się za to zabrać ? 1. Osoba X wykonuje pracę w ciągu 4, 5, albo 6−ciu godzin i może popełnić przy tym 0, 1 albo 3 błędy. Zakładając jednakowe prawdopodobieństwo dla każdego z 9−ciu zdarzeń jednoelementowych znaleźć prawdopodobieństwa następujących zdarzeń: a). Praca zostanie wykonana w ciągu 4 godzin (zdarzenie A). b). Praca zostanie wykonana bezbłędnie w czasie 6 godzin (zdarzenie B). c). Praca zostanie wykonana w czasie 5 godzin najwyżej z jednym błędem (zdarzenie C). d). Praca zostanie wykonana z co najwyżej jednym błędem (zdarzenie D).

RJS: :(

52: A nie będzie jakoś tak prościutko ? Masz do tego odp ?

	1
a)
	3

	1
b)
	9

tak intuicyjnie...

RJS: Nie mam odpowiedzi.

Lutek: Nie miałem kombinatoryki jeszcze w szkole ale na chłopski rozum to powinno być tak: Masz wszystkich 9 zdarzeń: 4 godziny i 0 błędów / 4 godziny i 1 błąd / 4 godziny i 3 błędy 5 godzin i 0 błędów / 5 godzin i 1 błąd / 5 godzin i 3 błędy 6 godzin i 0 błędów / 6 godzin i 1 błąd / 6 godzin i 3 błędy a)praca wykonana w 4 godziny (nie ważne czy z błędami czy nie) szansa 1/3 b)praca w 6 godzin bezbłędnie to odpowiada temu tylko 1 przypadek z 9 czyli szansa 1/9 c)praca w 5 godzin z najwyżej 1 błędem czyli może być 1 błąd lub 0 błędów więc odpowiadają 2 przypadki z 9 więc szansa 2/9 d)czas jest nieważny i odpadają tylko opcje gdzie są 3 błędy czyli szansa 6/9 = 1/3 Tak mi się wydaje, chyba, że czegoś nie zrozumiałem

Lutek: w podpunkcie d 2/3 zamiast 1/3*

52: 6/9≠1/3

Lutek: literówka

RJS: Dzięki tamto już rozkminiłem a to wiecie jak ? 3. Trzy ściany czworościanu zostały pomalowane na biało, czerwono i zielono zaś czwarta w pasy biało−czerwono−zielone. Doświadczenie polega na rzucaniu czworościanu na płaszczyznę i obserwowaniu koloru ściany, na którą upadł czworościan. Zdarzenia B, C, Z są określone następująco: − B – ściana biała, − C – ściana czerwona, − Z – ściana zielona. Sprawdzić czy zdarzenia B, Z, C są: niezależna parami.

RJS: Mila ?

RJS:

RJS:

Qulka: cała ściana czy że występuje dany kolor ?

Qulka: nie są niezależne bo 1/4 •1/4 ≠ 1/4

Qulka: lub jeśli uznać że liczymy kolorowe to 2/4 • 2/4 = 1/4 więc są

Qulka: i to drugie chyba będzie właściwsze chociaż treść tak do końca na to nie wskazuje

RJS: Qulka pomożesz jeszcze trochę ?

Mila: 3) Dziwnie sformułowane, jeśli upadnie na pasy to zdarzenie A∩B∩C ?

	1
P(B)=
	4

	1
P(Z)=
	4

	1
P(B∩C∩Z)=		?
	4

	1
P(B)*P(Z)=
	16

	1		1
P(B∩Z)=		≠		nie są
	4		16

Nie mam pewności.

RJS: 10. W pojemniku są kule białe i zielone. Losujemy 3 razy po jednej kuli ze zwracaniem. A – polega na wylosowaniu przynajmniej jednej kuli białej B – polega na wylosowaniu przynajmniej dwóch kul zielonych. Opisać Ω, A∪B, A∩B, A \ B,A', B' , sprawdzić prawa de Morgana Czy mogę to opisać ? b−białe z−zielone

	z 2		b 1		z 1		b 2		b 3
A=		*		+		*		+

	z 2		b 1		z 3
B=		*		+

Ale jak zrobić reszte polecenia ?

Qulka: w A jeszcze 3 białe

Qulka: aaa widzę ..jest tam

Qulka:

	z+b 3
Ω=

Qulka:

	z 3
AuB to A +

	z 2		b 1
AnB to		•

Qulka: A/B to te A bez części wspólnej = B' (tak od razu)

	z 3
A' =

RJS: Dziękuję, nie przesadzę jak wstawię jeszcze 4 zadania ?

RJS: Rozpatrujemy ilość wody (dm3) jaką może mieć do przeprowadzenia betonowy przepust. Dotychczasowe obserwacje pozwalają przyjąć, że: −P(A) – prawdopodobieństwo, że ilość wody (na sekundę) przyjmie wartość z przedziału (125, 250) wynosi 0,6, −P(B) – prawdopodobieństwo, że ilość wody (na sekundę) przyjmie wartość z przedziału (200, 300) wynosi 0,7 a P(A∪B)=0,8. Obliczyć prawdopodobieństwa P(A' ), P(B' ), P(AB), P(A'B' ), P(BA' ), P(B∪A' ). P(A')=0,4 P(B')=0,3 P(AB)=0.42 P(A'B')=0,12 P(B∪A') ? tego nie umiem policzyć

Qulka: P(A∪B) =P(A) + P(B) − P(AnB) więc P(AnB) = 0,5 zatem P(B∪A') = P(A')+P(AnB) = 0,4+0,5 =0,9

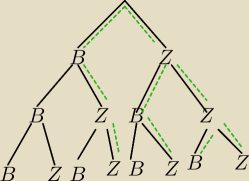
Mila: Losujemy ze zwracaniem więc nie możesz stosować kombinacji. Nie o to pytają. Ω={(B,B,B),(B,B,Z),(B,Z,B),(B,Z,Z)(Z,B,B),(Z,B,Z),(Z,Z,B),(Z,Z,Z)} (B,Z,B) oznacza − za pierwszym razem wylosowano kulę białą , za drugim zieloną , za trzecim kulę białą A – polega na wylosowaniu przynajmniej jednej kuli białej A={(B,B,B),(B,B,Z),(B,Z,B),(B,Z,Z),(Z,B,B),(Z,B,Z),(Z,Z,B)} B− polega na wylosowaniu przynajmniej dwóch kul zielonych. B={(B,Z,Z),(Z,B,Z),(Z,Z,B),(Z,Z,Z)} A∩B={(B,Z,Z),(Z,B,Z),(Z,Z,B)} A\B={(B,B,B),(B,B,Z),(B,Z,B),(Z,B,B)} Poradzisz sobie dalej?

RJS: Tak, dziękuję chyba dalej dam radę. Ale ma jeszcze sporo pytań, przepraszam, że o tej godzinie wstawiam zadania, ale wcześniej nie było czasu z powodu zajęć na uczelni

Mila: 00:04 to zadanie 10

Mila: Dobranoc . Wpisuj, jutro spojrzę. Sprawdź na drzewku, bo w tym edytorze słabo widać. Do jutra.

RJS: 4. Na przenośnik taśmowy trafiają jednakowe produkty wytwarzane przez dwa automaty. Stosunek ilościowy produkcji pierwszego automatu do produkcji drugiego jest równy 3:2. Pierwszy automat wytwarza średnio 65% produktów pierwszej jakości drugi zaś 85%. Spośród produktów na przenośniku pobieramy losowo jeden. a). Obliczyć prawdopodobieństwo, że będzie to produkt pierwszej jakości. b). Losowo wybrany produkt okazał się pierwszej jakości. Mógł on zostać wyprodukowany przez pierwszy lub drugi automat. Które zdarzenie jest bardziej prawdopodobne. Tutaj nie mam pomysłu

Qulka: też drzewko

RJS: Ale tutaj mam jakieś stosunki...

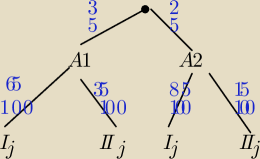
Qulka: że I jakości 3/5•0,65 + 2/5 • 0,85 = 0,73 warunkowe że 1A 0,39/0,73 = że 2A 0,34/0,73 = bardziej że 1Automat

Qulka: stosunki dodaj i podziel

RJS: Dziękuję bardzo ! teraz już dokończę sobie sam