funkcja
ciapek: f(A)=?
f−1(B)=?
A=(0,3>
B=<2,4>
f(x)=|2x−1|+1
Jak rozwiązywać takie zadania?
19 paź 20:05
sushi_gg6397228:
zacznij od rysunku f(x)= |2x−1|+1
19 paź 20:44
ciapek: Rysuję i potem tylko patrzę na zbiór wartości w tym przedziale?
Czyli f(A)=<1,6>
f(B)=<4,8>?
19 paź 21:54
sushi_gg6397228:
F(A) masz podane "x" i szukasz "y"
f−1 (B) masz podane "y" i szukasz "X"
19 paź 21:56
sushi_gg6397228:
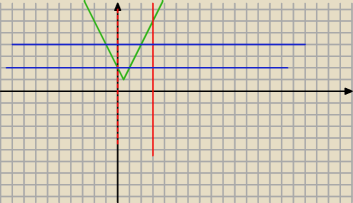
19 paź 21:57
ciapek: Tak, już wszystko rozumiem, zapomniałem, że w B jest przeciwdziedzina.
Dziękuję za pomoc

19 paź 22:05
sushi_gg6397228:
na zdrowie

19 paź 22:06
ciapek: A przy okazji jak wyznaczać przeciwdziedzinę? Póki co zauważyłem, że jeśli nie jest powiedziany
z góry, że to jakiś przedział to zawsze jest to R. Są jakieś wytyczne jak wyznaczać
przeciwdziedzinę?
19 paź 22:07
sushi_gg6397228:
Trzeba znać dziedzinę oraz ZW standardowych funkcji i wiedzieć jak wyglądają wykresy
w tym zadaniu, jakby nie podali A, tylko x ∊R, to z wykresy ZW= < 1; ∞)
co do zbioru B− to f. wyjściowa musiałaby być "na"
na studiach zabawa jest zawsze w zbiorach podanych przedziałami liczbowymi
19 paź 22:11
ciapek: Jeszcze jedno, ostatnie już pytanie o badanie suriekcji. Jeśli mam jakiś pierwiastek czy
wartość bezwzględną to od razu wiadomo, że nie jest, ale co w przypadku mniej oczywistych
funkcji?
Bierzemy dowolny x, podstawiamy i sprawdzamy czy to co otrzymaliśmy ma sens?
19 paź 22:26
b.: > Jeszcze jedno, ostatnie już pytanie o badanie suriekcji. Jeśli mam jakiś pierwiastek czy
wartość bezwzględną to od razu wiadomo, że nie jest
?
Np. f(x)=|x| jako funkcja z R do [0,∞) jest surjekcją.
g(x)=ln|x| jako funkcja z R\{0} do R jest surjekcją.
19 paź 22:30
ciapek: Na odwrót chyba, bierzemy dowolny y i patrzymy czy wyjdzie x, tak?
19 paź 22:31
ciapek: @b. W domyśle chodziło mi o takie, gdzie nie ma określonej przeciwdziedziny przedziałem i wtedy
te funkcji, które wymieniłeś nie byłyby surjekcją, przynajmniej na pewno pierwsza.
19 paź 22:33
b.: @22:31: no z grubsza tak
@22:33: trochę to słaba reguła, np. ln(√x) z naturalną dziedziną i przeciwdziedziną=R jest
surjekcją. Trzeba sprawdzać.
19 paź 23:04
ciapek: Masz rację

Jeszcze taki typ zadań:Znajd´z funkcje, z których utworzone są następujące funkcje złożone:
f(x) = (2x
2 + x + 1)
4
Czy będzie to coś takiego:
f(x)og(x)
f(x)=x
4
g(x)=2x
2+x+1
19 paź 23:27
b.: Może być, z tym, że zadanie ma mnóstwo rozwiązań. To Twoje jest jednak naturalne.
20 paź 20:25



 Jeszcze taki typ zadań:Znajd´z funkcje, z których utworzone są następujące funkcje złożone:
f(x) = (2x2 + x + 1)4
Czy będzie to coś takiego:
f(x)og(x)
f(x)=x4
g(x)=2x2+x+1
Jeszcze taki typ zadań:Znajd´z funkcje, z których utworzone są następujące funkcje złożone:
f(x) = (2x2 + x + 1)4
Czy będzie to coś takiego:
f(x)og(x)
f(x)=x4
g(x)=2x2+x+1