W równoległoboku ABCD, zaznaczono punkt E, który dzieli bok AB na pół., a na boku AD odłożono
taki punkt F, że 3|AF|=|AD|. Wyznacz stosunek w którym prosta EF dzieli przekątną AC.
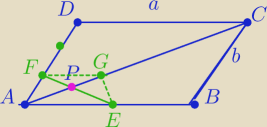3|AF|=|AD|
SZukane:
| |AP| | |
=? | |
| |PC| |
| 1 | 1 | |||
ΔAFG∼ΔADC w skali k= | ⇔|FG|= | a | ||
| 3 | 3 |
| 2 | |||||||||
ΔFGP∼ΔAEP w skali k1= | = | |||||||||
| 3 |
| 1 | ||
|AG|= | |AC| | |
| 3 |
| 1 | ||
5x= | |AC| | |
| 3 |
| |AC| | ||
x= | ||
| 15 |
| |AC| | ||
|AP|=3x= | ||
| 5 |
| |AC| | 4|AC| | |||
|PC|=|AC|− | = | |||
| 5 | 5 |
| |AP| | 1 | ||
= | |||
| |PC| | 4 |
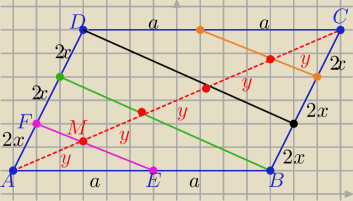Wszystkie odcinki są równoległe i dzielą przekątną AC na 5 równych części
to:
|AM|: |AC|=1:5