Wyznacz zbiór X z równania A U X = B BadWolf: Cześć Mam takie zadanie z logiki: Dane są dwa zbiory A i B. Rozwiązać równanie A U X = B. Nie mam zielonego pojęcia jak wyznaczyć zbiór X z tego równania. Kilka pomysłów jakie miałem zostało odrzucone jako błędne i w tym momencie stoję w miejscu. Czy ktoś jest w stanie to zadanie rozwiącać?!

Przemysław: X=B\A ?

Przemysław: Nie, to było nieprzemyślane

BadWolf: Z tego co wiem to X=B\A jest błędne, a przynajmniej tak mi powiedział mój profesor. Nie mam jednak pojęcia co innego mogłoby być rozwiązaniem.

Przemysław: To jest błędne, bo B\A odejmuje też A∩X a tego nie chcemy odejmować

Benny: Narysuj sobie zbiory to może coś zauważysz.

BadWolf: Gapiłem się na wykresy Venn'a przez dobre pół godziny i nic nie zauważyłem. Nie jestem w stanie zapisać niczego sensowniego, chyba że te zbiory są rozłączne.

Janek191: Jeżeli [ A ∩ X = ∅ ∧ A ∪ X = B ] ⇒ X = B \ A

BadWolf: Tak ale co jeśli A∩X≠∅. Właśnie w tym miejscu stoję.

Janek191: Zdaje się,że nie da się tego sensownie zapisać, bo X występuje po obu stronach równości

BadWolf: Zastanawiałem się jeszcze czy [ A∪X=B ⇔ A∩X=∅ ], ale musiałbym to udowodnić, co też stanowi dla mnie wyzwanie ponad siły i wiedzę.

trutututu: A⊂B i X⊂B jeśli A nie zawiera się w B to równanie jest sprzeczne

trutututu: w drugą stronę B⊂A∪X ⇒B⊂A lub B⊂X z pierwszego i drugiego A⊂B i X⊂B i (B⊂A lub B⊂X)⇒A=B i X⊂B lub X=B i A⊂B

BadWolf: Tyle to wiedziałem od początku. Tu chodzi o wyznaczenie X za pomocą A i B. Zastanawiam się czy [ A∪X=B ⇔ A∩X=∅ ], jak zresztą napisałem wcześniej, a nie o to czy A i X ⊂ do B.

trutututu: to bez sensu, to nie jest równanie z niewiadomą x tylko równość zbiorów

BadWolf: jeśli B⊂(A∪X) to z tego nie wynika, że B⊂A lub B⊂X; A⊂B i X⊂B i (B⊂A lub B⊂X) jest nie możliwe, bo jeśli A⊂B i X⊂B to B nie może należeć do żadnego z nich

trutututu: nieprawda

BadWolf: Zadaniem jest znalezienie X. Np. to co było powiedziane wcześniej X=B\A, ale to działa tylko jeśli A∩X=∅, więc pozostaje jeszcze 2 przypadek.

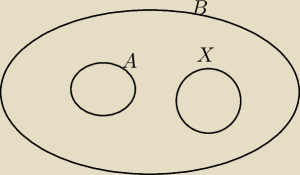
BadWolf: Jeśli A⊂B i X⊂B to nie ma opcji aby B⊂A lub B⊂X

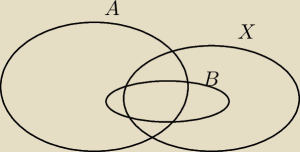
BadWolf: Podobnie tu jeśli B⊂(A∪X) to z tego nie wynika, że B⊂A lub B⊂X

trutututu: to nie jest poprawne rozumowanie

BadWolf: Jeśli ktoś ma pomysł to byłbym bardzo wdzięczny z podzielenie się nim.

trutututu: pomyśl nad tym co napisałem o 19.38 tylko takie sytuacje możesz rozpatrywać

BadWolf: W takim razie powiedz mi, dla czego, a nie pisz, że nie mam racji bez żadnego uzasadnienia

BadWolf: Pokazałem ci na prostych wykresach, że to co piszesz jest sprzeczne. Jeśli nie jest to pokaż mi dla czego, bo chyba nie jest zaskakującym , że nie rozumiem tego zadania

trutututu: po lewej i prawej stronie równości masz dwa zbiory, które mają być sobie równe A∪X=B to równanie jest prawdziwe ⇔ A∪X⊆B i A∪X⊇B ( nie widziałem, że jest tutaj taki symbol)

trutututu: gubisz się i nie możesz zrozumieć zadania bo robisz nieodpowiednie rysunki

BadWolf: Co do A∪X⊆B się zgadzam, bo jest to dla mnie oczywiste, ale jeśli A∪X⊇B oznacza B⊆A∪X to wracamy z powrotem do A∪X=B, co nic nie daje

BadWolf: Jeśli chodzi o rysunki to pokazują one przypadki, w których nie masz racji

trutututu: ech, nie, że nie mam racji, tylko pokazują sytuacje gdy nie ma równości

BadWolf: Nadal nie jestem w stanie napisać nic o zbiorze X. Jeśli masz rację to należy uzasadnić, dla czego odrzucam część przypadków czego jeszcze nie zrobiliśmy.

trutututu: To już zrobiłem ale Ty jak widać nie wierzysz i nadal upierasz się przy tych rysunkach, z których niczego wywnioskujesz

BadWolf: Jeśli masz rację to należy uzasadnić, dla czego odrzucam część przypadków czego jeszcze nie zrobiliśmy. Co mam napisać, jako uzasadnienie. Musisz mi to powiedzieć, bo nie widzę tego.

BadWolf: Jeśli kogoś interesuje rozwiązanie to, zgodnie z wypowiedzią autora zadania, nie da się go dokładnie dookreślić, natomiast X=B\A to najmniejszy możliwy zbiór z tych, które mogą być rozwiązaniem, no i oczywiście X=B to największy możliwy (zakłądając, że A⊆B ∧ X⊆B).