trapez ewa: Podstawy trapezu mają długości a i b. Wyznacz długość odcinka łączącego środki przekątnych trapezu

ewa:

Basia: Pomagam

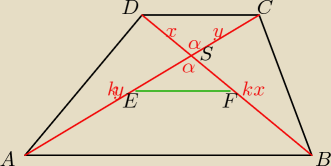
Basia: trójkąty ASB i CSD są podobne w skali k=^a_b stąd można przyjąć tak jak na rysunku DS=x i BS=kx CS=y i AS=ky BD = x+kx = (k+1)*x F jest środkiem BD ⇒ BF = ^(k+1)*x₂ FS = BS−BF =kx − ^(k+1)x₂ = ^2kx−(k+1)x₂ = ^{x(2k−k−1)}₂ = ^x(k−1)₂ analogicznie wyliczymy, że ES = ^y(k−1)₂ z tw.cosinusów EF² = ES²+SF²−2ES*FS*cosα =

y2(k−1)2		x2(k−1)2		xy(k−1)2
	+		− 2*		*cosα=
4		4		4

(k−1)2
	*(y2+x2−2xy*cosα) =
4

(k−1)2
	*CD2 =
4

(ab−1)2
	*b2 =
4

(a−bb)2
	* b2 =
4

(a−b)2
	*b2 =
4b2

(a−b)2
4

EF = √^(a−b)2₄ = ^|a−b|₂

ewa: Dziękuje za pomoc i wylumaczenie