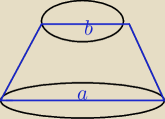
Przekrojem osiowym stożka ściętego (rysunek wyżej) jest trapez równoramienny o kącie ostrym α i
podstawach a i b (b<a). Uzasadnij, że objętość tego stożka jest równa 1/24π(a3 − b3)tgα
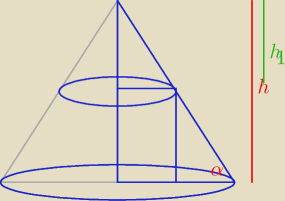
| a | h | |||
Skala podobieństwa między stożkami: k = | = | |||
| b | h1 |
| h | a | |||||||||
tgα = | ⇒ h = | tgα | ||||||||
| 2 |
| bh | b | |||
h1 = | = | tgα | ||
| a | 2 |
| 1 | 1 | a | 1 | |||||
V = | π( | a)2 * | tgα = | πa3tgα | ||||
| 3 | 2 | 2 | 24 |
| 1 | 1 | b | 1 | |||||
V1 = | π( | b)2 * | tgα = | πb3tgα | ||||
| 3 | 2 | 2 | 24 |
| 1 | ||
V − V1 = | π(a3 − b3)tgα | |
| 24 |
