Wymień ciapek: Wymień elementy zbioru A={x:x³ − 3x³ − |4x − 12| =0

Mila: Chyba coś źle przepisałeś?

Sun: Tak przepraszam, już poprawiam...

ciapek: Już piszę poprawne

ciapek: A={x:x³ −3x² − |4x−12|=0

pigor: ..., A={x∊R : x³−3x²−|4x−12|=0} , to x³−3x²−|4x−12|=0 ⇔ x²(x−3)−4|x−3|=0 ⇔ ⇔ (x< 3 i x²(x−3)+4(x−3)=0) v (x ≥0 i x²(x−3)−4|(x−3)=0) ⇔ ⇔ (x< 3 i (x−3)(x²+4)=0) v (x ≥0 i (x−3)(x²−4)=0) ⇔ ⇔ (x< 3 i x=3) v (x ≥0 i (x−3)(x−2)(x+2)=0) ⇔ A={3,2,−2} . ...

ciapek: Też tak zrobiłem, ale to jest źle, poprawna odp. to 3

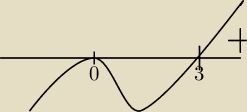
henrys: bo pigor sie pomylił x³−3x²=|4x−12| x²(x−3)≥0 x=0 lub x≥3 dla x=0 dostajemy sprzeczność dla x≥3 x³−3x²−4(x−3)=0 (x²−4)(x−3)=0 x=2 lub x=−2 lub x=3

ciapek: Piękna odpowiedź, bardzo dziękuję

pigor: ..., fakt; tylko x=3 przez podstawienie spełnia dane równanie a ja w ostatniej linijce nie wiem dlaczego nie wyrzuciłem x= −2, natomiast dlaczego x=2 też nie spełnia danego równania jeszcze ... "nie widzę" .

pigor: ...,teraz już ... widzę, nie wiem skąd mój warunek x ≥0 w przedostatniej linii , zamiast x ≥3 ; przepraszam

ciapek: Najważniejsze, że w końcu udało się dojść do wyniku