Zilustruj zbiór punktów, których współrzędne spełniają podane równanie Stark: Zilustruj w układzie współrzędnych zbiór punktów, których współrzędne spełniają równanie: a) |x+3|+|y−2|=1 b) |x−1|−|y+3|=2 Proszę o pomoc albo chociaż wskazówki od czego zacząć..

ICSP: a) Wiesz jak wygląda |x| + |y| = 1 ?

Stark: Nie wiem

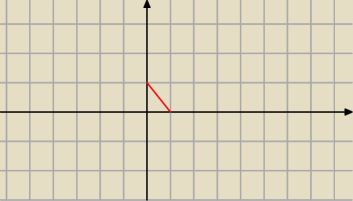
ICSP: No to rozpisz IV przypadki. 1^o x > 0 oraz y > 0 : x + y = 1 ⇒ y = −x + 1 Pozostałe 3 zostawiam tobie. Potem wystarczy zauważyć, że |x + 3| + |y − 2| = 1 jest przesunięciem |x| + |y| = 1 o wektor [−3 , 2]

Stark: czyli wychodzi, że: 2◯ x−y=1 ⇒ y=x−1 3◯ −x+y=1 ⇒ y=x 4◯ −x−y=1 ⇒ y=−x−1 Niestety nie umiem przesunięć wykresów, ominęłam cały dział

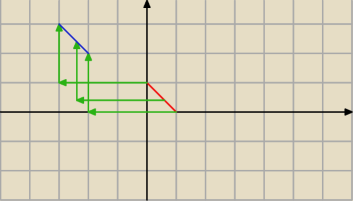
ICSP: Przesuwam czerwony odcinek o 3 w lewo oraz o 2 w górę i dostaje odcinek niebieski. W taki sam sposób przesuniesz resztę i dostaniesz "kopnięty" kwadrat.

Stark: Okej, chyba rozumiem Czyli w przykładzie b rozpisuję sobie |x|−|y|=2, rysuję to na osi, a później przesuwam o wektor [1,−3]?

ICSP: Oczywiscie możesz też robić bez przesuwania i rozpisywać przypadki x> 3 oraz y > 2 itd. , ale moim zdaniem łatwiej jest właśnie przesuwajac.

Stark: Faktycznie, jest łatwiej. Dziękuję, jestem bardzo wdzięczna! Zrozumiałam i już wszystko wychodzi