Interpretacja geometryczna (liczby zespolone)
tony67: Cześć!
Chciałbym Was dopytać o kwestię narysowania poniższego zbioru (z należy do liczb zespolonych)
|z−1| = Re(z+1)
Jak to interpretować?
Odległość z od jedynki ma być równa części rzeczywistej z + 1.
Czyli to będzie punkt (0,1)? Jak to sobie najlepiej wytłumaczyć? Zwłaszcza prawą stronę.
Z góry dziękuję.
18 paź 03:41
sushi_gg6397228:
podstaw
z=x+iy
z−1= (x−1) + iy
z+1= (x+1) + iy
|z−1|=...
Re(z+1)=...
18 paź 09:00
tony67: Czy to jest poprawnie?
|x+yi−1|=x+1
(x−1)2+y2=(x+1)2
x2−2x+1+y2=x2+2x+1
−4x+y2=0
y2 = 4x
19 paź 20:56
sushi_gg6397228:
+ założenia że obie strony są dodatnie−> tam gdzie podnosiłeś do kwadratu
tak to wychodzi
19 paź 21:15
tony67:
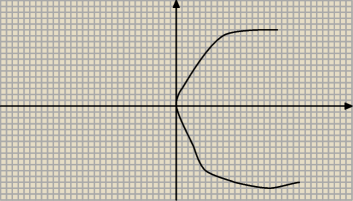
Dziękuję za odpowiedź.
Czyli 1 założenie
x + 1 > 0
x > −1
oraz
x+yi−1 > 0
x + yi > 1
Będzie miało to wpływ na rysunek? Przepraszam za jakość tego, ale nie widzę możliwości
wstawienia obrazków (tak bardzo "ogólnie" wygląda mój rysunek).
19 paź 21:24
sushi_gg6397228:
|....| = √.... czy to zawsze jest nieujemne , więc x+1≥0, aby podnieść do kwadratu
i potem włączamy myslenie
19 paź 21:26
tony67: Fakt, druga kwestia zbędna.
Dla podsumowania:
x + 1 ≥ 0, aby moduł był co najmniej zerowy
x ≥ −1
Przy czym rysunek zaczyna się w (0,0), więc na samym rysunku chyba nie mam już niczego więcej
do zaznaczenia?
19 paź 21:32
sushi_gg6397228:
Tak na przyszłość:
zawsze można sprawdzić; wziąć parę punktów z wykresu i podstawić do wyjściowego przykładu
19 paź 21:34
Mila:
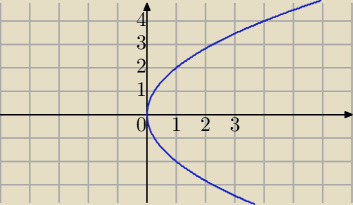
19 paź 21:36
tony67: Dziękuję za odpowiedź. Bardziej chodziło mi o to czy to założenie jest konieczne czy jest to
bardziej kwestia dokładności, bo w praktyce i tak kwadrat nie mógłby być ujemny.
19 paź 21:53
Mila:
Nie jest konieczne.
19 paź 22:36
Mila:
Masz y2=4x to jest parabola o poziomej osi symetrii.
19 paź 22:37
 Dziękuję za odpowiedź.
Czyli 1 założenie
x + 1 > 0
x > −1
oraz
x+yi−1 > 0
x + yi > 1
Będzie miało to wpływ na rysunek? Przepraszam za jakość tego, ale nie widzę możliwości
wstawienia obrazków (tak bardzo "ogólnie" wygląda mój rysunek).
Dziękuję za odpowiedź.
Czyli 1 założenie
x + 1 > 0
x > −1
oraz
x+yi−1 > 0
x + yi > 1
Będzie miało to wpływ na rysunek? Przepraszam za jakość tego, ale nie widzę możliwości
wstawienia obrazków (tak bardzo "ogólnie" wygląda mój rysunek).
