Narysuj zbiór punktów spełniających nierówność Xyna: Narysuj zbiór punktów spełniających nierówność |x+1|+|y+2|≤2

sushi_gg6397228: i co zaproponujesz ?

Xyna: Rozdzielilabym n funkcje y=|x+1| i y= 2−|y+2| tylko w tej drugiej nie jestem pewna oznaczeń tzn y w module jest wartością i tylko wartością czy dodatkowo funkcja f (x)

sushi_gg6397228: trzeba rozpatrzec 4 przypadki + + + − − + − −

Xyna: Gdyby w miejscu modułu |y+2| był moduł |x+2| rozpatrywane by były trzy przypadki prawda? Tzn 1 (−∞,−2) <−2,−1> (−1,+∞), ale skoro mam y to załóżmy rozpatrujemy 1 przypadek − − , czyli −×−1−y−2≤2 czyli y≥−(x+1) czyli właściwie co to znaczy

ICSP: Ja zaproponuje takie podejści : Wiemy, że (*) : |x| + |y| ≤ 1 jest kopniętym kwadratem. Wiemy również jak z (*) zrobić (**) : |x| + |y| ≤ 2. To co karzą Ci narysować jest tylko przesunięciem każdego punktu (**) o wektor [−1 , −2]

Eta:

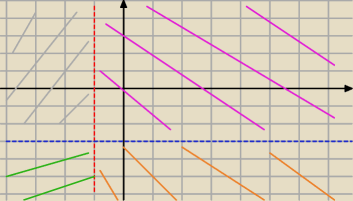
sushi_gg6397228: masz "4" kolorowe ćwiartki i potem rozwiazanie każdego przypadku musi siedzieć w każdej ćwiartce

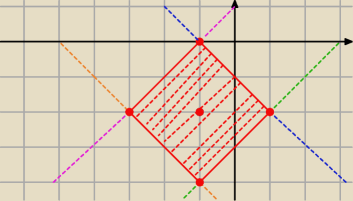
PW: Dodam komentarz do "słów" Ety z 20:25, czyli odpowiem na pytanie "A skąd ja miałbym być taki mądry?" Nierówność |x+1| + |y+2| ≤ 2 oznacza, że dwie liczby nieujemne mają sumę mniejszą lub równą 2. Rysujemy przypadki "skrajne" − gdy y = − 2, to suma jest równa 2,dla |x+1| = 2, czyli dla x = 1 lub x= − 3. Mamy więc dwa "skrajne" punkty: (−3, −2) i (1, −2). Nazywam je skrajnymi, gdyż w zadanym zbiorze w sposób oczywisty nie może być punktów o pierwszej współrzędnej mniejszej niż −3 ani większej niż 1. Podobnie wyznaczamy dwa skrajne punkty o pierwszej współrzędnej równej −1: (−1, 0) i (−1, −4). Łączymy skrajne punkty odcinkami i mamy brzeg szukanego obszaru ograniczonego. Dlaczego jego brzeg składa się z odcinków − znowu oczywiste, każda z nierówności na jakie możemy podzielić badaną nierówność, by nie miała wartości bezwzględnych, jest nierównością typu y ≤ ax + b lub y ≥ ax+ b.

Xyna: Czemu skrajność jest w (−2) ? Tak mało ogarniam ale poważnie tego nie widzę, btw mam 17 lat

PW: Chcesz zobaczyć ten ostatni kwadrat metodą opisaną wyżej o 21:11? |x| + |y| ≤ 2 Dla y = 0 mamy |x| ≤ 2, a więc skrajnymi wartościami iksa, dla których nierówność jest spełniona, są x = −2 oraz x= 2. W ten sposób widzimy dwa punkty, które należą do badanej figury: (−2, 0) i (2, 0). Podobnie myślimy o igrekach w sytuacji, gdy x = 0.

Xyna: Aaaaaa, genialne dziękuję bardzo

Eta: Co tu takiego "genialnego" ?

Xyna: Prostota stylu

Xyna: Tzn teraz załapałam, i wszystko co było wyżej było kosmosemm a wystarczyło tylko to ze jeden z modułów ma równać się 0 i dalej idzie