Zilustruj zbiór na płaszczyźnie zespolonej luX: Hej! Mam problem z jednym zadaniem z liczb zespolonych: Zilustruj na płaszczyźnie zespolonej zbiór: {z: |z−2i| / |z+3| < 1} Próbowałem kilka razy, za z podstawiam x+yi i wymnażam nierówność przez |z+3| jednak ciągle wychodzi mi wykres który jest inny niż ten w odpowiedziach i rozwiązaniu kogoś innego, byłbym bardzo wdzięczny za pomoc

sushi_gg6397228: najpierw policz |Z+2i|=...

sushi_gg6397228: tak miało być: |z−2i|=...

PW: No dobrze, a jaka jest interpretacja geometryczna zbioru {z: |z − 2i| = r₁} , r₁∊R i r₁ ≥ 0 ?

Janek191: Może tak :

I x + y i −2 i I
	< 1
I x + y i + 3 I

I x + ( y − 2) i I
	< 1
I (x + 3) + y i I

I x + ( y − 2) i I < I ( x + 3) + y i I √ x² + y² − 4 y + 4 < √ x² + 6 x + 9 + y² x² + y² − 4 y + 4 < x² + 6 x + 9 + y² − 4 y + 4 < 6 x + 9 − 4 y < 6 x + 5 / : ( − 4) y > − 1,5 x − 1,25 =============

luX: Jeśli o to chodzi to wierzę, że kolejnym krokiem jest przejście na: |x+i(y−2)|<|(x+3)+yi| PW, nie wiem jak odpowiedzieć na Twoje pytanie, czy w tej interpretacji chodzi tylko o część rzeczywistą skorą r1 należy do rzeczywistych?

luX: Janek191, z czego wynika to przejście w 4 linijce, możemy w dowolonym momencie zmienić moduły liczby zespolonej na odległość, a nastepnie liczyć bez pierwiastków? Jeżeli tak to już rysuje mi się obraz wykonywania tego typu zadań i dziękuję

Janek191: z = a + b i to I z I = I a + b i I = √ a² + b²

PW: Do uwagi z 19:29. To ja się dziwię, że o to pytasz. Przecież zadana nierówność tak naprawdę jest nierównością między liczbami rzeczywistymi. Moduły to liczby rzeczywiste.

luX: Tak, stosowałem to już w przeszłości, nie wiem czemu w momencie gdy zobaczyłem treść o płaszczyźnie zespolonej stwierdziłem że muszę zrobić coś innego. Dzięki za pomoc

Benny:

|z−2i|
	<1
|z+3|

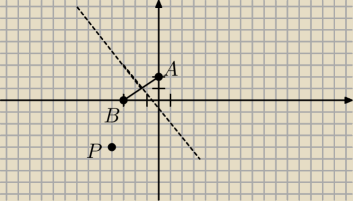
|z−2i|<|z+3| Wiemy, że |z−2i|=|z+3| to symetralna Weźmy jakiś punkt z płaszczyzny np. P(−4,−4) Jak widać odległość z P do B jest mniejsza jak z P do A, a to jest sprzeczne, więc bierzemy część płaszczyzny która jest nad symetralną.

Mila:

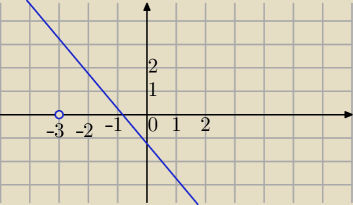
	|z−2i|
{z:		< 1}, z≠−3
	|z+3|

|z−2i|
	< 1⇔
|z+3|

|z−2i|<|z+3| zbiór punktów takich, że : |z−2i|=|z+3| to symetralna odcinka A=(0,2) i B=(−3,0) (x−0)²+(y−2)²=(x+3)²+y² x²+y²−4y+4=x²+6x+9+y² −4y+4=6x+9 −4y=6x+5

	3		5
s: y=−		x−
	2		4

Teraz masz do wyboru półpłaszczyznę nad prostą albo pod prostą , jak to ustalisz? (pomyśl)

Mila: Benny już odpowiedział.

Benny: Twoje rozwiązanie jest ładniejsze

Janek191: Zabrakło mi założenia : z ≠ − 3