Pole rombu jest równe 7.5 ert: Pole rombu jest równe 7.5 , a długość jego przekątnych różni się o 2. Wykaż, że tangens połowy kąta rozwartego tego rombu jest równy 5/3. Nie było mnie na tych zajęciach w szkole proszę o pomoc nie wiem jak się do tego zabrać.

Bogdan: Pierwszy krok − narysuj romb i oznacz go, zapisz opisane w zadaniu zależności. Pokaż rysunek i zależności tutaj.

ert: niestety nie mam pojęcia jak na tej stronce narysować ten romb , na karce wyszedł mi piękny latawiec

Bogdan: Kliknij przycisk rysuję, to ostatni przycisk nad polem tekstowym

ert: jest tylko kropka pomarańczowa i nic nie chce narysować

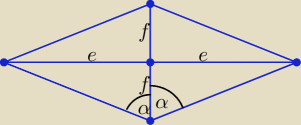
Bogdan: Ja narysuję, a Ty powtórz ten rysunek

Bogdan: No dobrze, zapisz zależności określone w zadaniu przy pomocy oznaczeń z mojego rysunku.

Bogdan: Mam odczucie, że liczyłeś na gotowca. Dobranoc

ert: Dziękuję za piękny rysunek nie nie liczyłam na gotowca bo nie mam pojęcia od czego mam zacząć nie było mnie na zajęciach a z podręcznika nie mogę sama nic zrobić

ert: Proszę o pomoc w rozwiązaniu tego zadania nie wiem co dalej z tym zrobić ,

sushi_gg6397228: zrób rysunek

Eta: Z rys. podanego przez Bogdana i z treści zadania:

	15
f= e+1 i P=		, e, f>0
	2

	1		15
P= 4*		e(e+1) =		⇒ 4e2+4e−15=0 Δ=256 , √Δ=16
	2		2

	−4+16		3		3		5
e=		=		to f=1+		=
	8		2		2		2

	f		5		2		5
tgα=		=		*		=
	e		2		3		3

ert: Dziękuję bardzo Eta , ale patrze na to gotowe rozwiązanie i niestety nie mam pojęcia co i skąd się wzięło posiedzę popatrzę i postaram się zrobić to krok po kroku nie pomyślałam aby obliczone pole 7,5 zapisać

	15
P=		i dlaczego f= e+1
	2

Przepraszam ale chcę to zrozumieć

sushi_gg6397228: w zadaniu podali przekatne róznią się o 2 2f−2e=2 / 2 f−e= 1 f=e+1

	15
7,5=
	2

ert: małymi krokami ale faktycznie dało się to ogarnąć, bardzo dziękuję za wyjaśnienie i pomoc nie było to łatwe zadanie bynajmniej dla mnie pozdrawiam serdecznie

Bogdan: Dobry wieczór ert, cieszę się, że nie oczekujesz gotowego rozwiązania, dodam z małym przekąsem − nieobecność w szkole w przypadku tego zadania nie jest przeszkodą do jego rozwiązania. Biorę mój nocny rysunek. 2e − 2f = 2 ⇒ e − f = 1 ⇒ e = f + 1 (to jest przecież oczywiste) Pole rombu P = U{1}[2}*2e*2f = 2ef (to też nie jest Ci obce) 2ef = 7,5 ⇒ 2f(f + 1) = 7,5 ⇒ 2f² + 2f − 7,5 = 0 (równanie kwadratowe, f > 0), Δ = 64 Wszystko dotąd jest banalne i znane Tobie.

	−2 − 8
f1 =		< 0 sprzeczność, bo długość nie jest ujemna
	4

	−2 + 8		3		3		5
f2 =		=		i e =		+ 1 =
	4		2		2		2

Zależności w trójkącie prostokątnym na pewno umiesz określić.

	e		5		2		5
tgα =		=		*		=		i tyle
	f		2		3		3

Czy nieobecność w szkole uniemożliwiła Ci przeprowadzić takie działania?

Bogdan:

	1
P =		*2e*2f = 2ef
	2

Eta:

ert: tak przeprowadzenie takiego działania po 20 letniej przerwie w szkole zrobiło mi trudność ;₎ Pozdrawiam