Trygonmetria K: Witam, pomoże ktoś zapamięta/ zakodować sobie w głowie, albo najlepiej wytłumaczy jak do tego dojść samemu? Gdy mamy wykresy : 1)f(x)= tg|x − π/3| 2) g(x)=tg ( |x| − π/3 ) to przy f(x) najpierw rysujemy wykres tg|x|, a potem przesuwamy o wektor , a przy g(x) najpierw przesuwamy o wektor a dopiero potem rysujemy tg|x| . i mam problem z wbiciem sobie do łba kolejności, bym nigdy przypadkiem nie narysował źle (nie pomylił czy rysowac najpierw wartość bezwględną czy przesunąć o wektor)

PW: To nie problem zapamiętać 2) tg(|x|) to to samo co tgx dla dodatnich x, a dla ujemnych x rysujemy "lusterko" względem osi OY. Gdy już wiemy jak wygląda tg(|x|), to przesuwamy by uzyskać tg(|x| − α)

K: tyle, że przy wykresie tg(|x| − a )najpierw przesuwamy a potem "odbijamy" wykres funkcji z prawej na lewą

PW: 1) Gdyby x − α > 0, to wartość bezwzględna nic by nie zmieniała, czyli dla x > α rysujemy "normalną" funkcję tg(x − α) − najpierw tg(x), potem przesuwamy równolegle do osi OX.. Dla x < α wykres jest symetryczny względem prostej x = α. Mówiąc "po chłopsku" wykres jest taki sam dla argumentów symetrycznych względem tego punktu, w którym x − α zeruje się.

PW: K

K: https://www.wolframalpha.com/input/?i=tg|x-pi%2F3| , widzisz tu " 1)f(x)= tg|x − π/3| " najpierw rysujemy tg (|x|) a potem przesuwamy, a przy "2) g(x)=tg ( |x| − π/3 )" najpierw przesuwamy a potem odbijamy. Zawsze można sprawdzić jak się nie jest pewnym podkładając jakąś liczbę, ale wolałbym nie stosować sprawdzania tylko być pewien jak rysować > .. <

PW: No, przestawiłem sobie w głowie i źle tłumaczę, dziękuję K − wiedziałeś sam, niepotrzebnie pytasz.

K: Chodzi o to, że ja nie do końca jestem pewien tego i boję się, że jak mi się powtórzy takie zadanie to źle zrobię i potrzebuję jakoś sobie to wbić do głowy na amen, bym był już zawsze pewien rozwiązania bo nie wystarczy zadanie zrobić, ale trzeba je w 100% zrozumieć

PW: Tak jeszcze myślę jak 2) wytłumaczyć (sobie ) najprościej: − Funkcja jest parzysta, f(−x) = f(x), czyli ma wykres symetryczny względem osi OY − wystarczy narysować dla x ≥ 0 i zastosować symetrię.

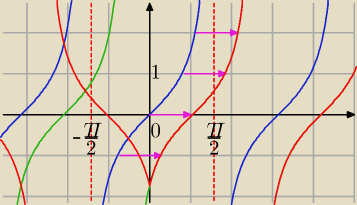
Mila: " Zwiąż" to z translacją. 1) Wzór funkcji po przesunięciu wykresu f(x) o wektor [a,0] to f(x−a) a) Zatem jeśli narysujesz wykres funkcji:

	π
y=tg(|x|) to po przesunięciu o wektor [		,0] otrzymasz wykres funkcji:
	3

	π
g(x)=tg(|x−		|)
	3

	−π		π
b) Masz wykres f(x)=tg(x) w przedziale (		,		)
	2		2

	π
to po translacji o wektor [		,0] otrzymasz wykres ⇒
	3

	π
g(x)=tg(x−		)→teraz symetria względem OY, tej części wykresu,
	3

która znajduje się po prawej stronie OY (z lewej idzie w zapomnienie)⇒

	π
h(x)=tg(|x|−		)
	3

K: Dzięki, mam nadzieję, że uda mi się to zapamiętać

Mila: